Key learning points

1. A spring is elastically deformed if it returns to its original shape after the applied force is removed
2. A spring is inelastically deformed if it does not return to its original shape after the applied force is removed
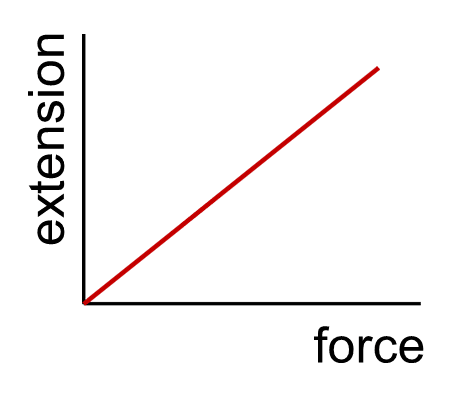
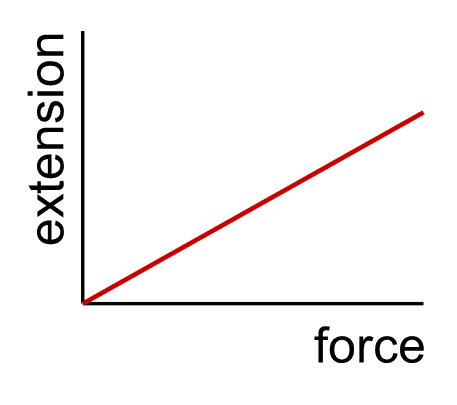
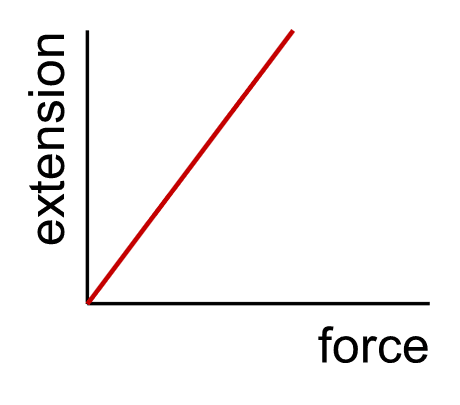
3. Elastic deformation is proportional to the force applied to stretch or compress a spring
4. The spring constant (k) is the force needed to extend or compress an elastic object by one metre
5. Force on a spring = spring constant × extension

Common misconception

Keywords

• Directly proportional - A variable is directly proportional to another if it doubles or triples when the other one does the same.

• Elastic deformation - The stretch of a spring that returns to its original shape when the stretching force is removed.

• Inelastic deformation - The stretch of a spring as it is permanently stretched out of shape.

• Spring constant - A measure of how stiff a spring is and how hard it is to stretch or compress.

• Hooke’s Law - For elastic deformations, extension (or compression) is directly proportional to the force applied.