Year 4
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- In this lesson, we will look at a range of representations for multiplications in the seven times table before creating our own concrete, pictorial and abstract representations. We will also briefly introduce commutative law when using written multiplication equations.
Licence
This content is made available by Oak National Academy Limited and its partners and licensed under Oak’s terms & conditions (Collection 1), except where otherwise stated.
5 Questions
Q1.
Which of the following numbers is not a multiple of 9?
108
171
72
Q2.
The 10 x 10 grid has been used to help represent the nine times table. But which multiple of 9 is circled?
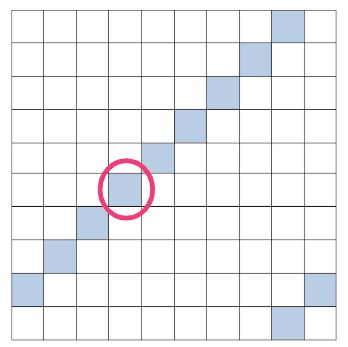
45
63
72
Q3.
During the lesson, we used a counting stick to help recite the nine times table. But what value is the arrow pointing at?

45
54
72
Q4.
Using my knowledge of the 9x multiplication table, I can find larger multiples of nine. But which of the following numbers is NOT a multiple of nine?
405
567
927
Q5.
Which of the following number sentences is incorrect?
9 x 10 = 18 x 5
9 x 4 = 3 x 12
9 x 6 = 27 x 2
5 Questions
Q1.
Using your knowledge of the 7x table, can you identify which of the following numbers is NOT a multiple of 7?
147
210
7007
Q2.
During the lesson we used a counting stick to represent the 7x multiplication table. What value is represented by the arrow?

14
21
35
Q3.
We used a blank grid to help represent the multiples of seven. Which multiple of seven is represented by the circle?
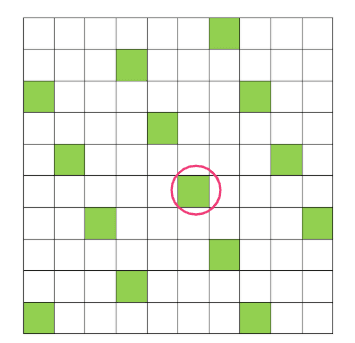
35
42
49
Q4.
Arrays are one such pictorial and concrete representation we can make to show multiplication facts. But which of the facts below is not shown by the array?

63 ÷ 7 = 9
7 x 3 x 3 = 63
7 x 9 = 63
Q5.
When solving a written equation such as 8 x 6, we are able to swap the order of the numbers so we can write it as 6 x 8. This a mathematical law known as:
Associative law
Distributive law
Multiplication law

