Myths about teaching can hold you back


- Year 5
Compare and describe measurements involving mass and capacity
I can compare and describe measurements involving mass and capacity.


- Year 5
Compare and describe measurements involving mass and capacity
I can compare and describe measurements involving mass and capacity.
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- A change in mass or capacity can be described multiplicatively.
- The sentence 'The __________ is ___ times the mass/capacity/volume of the __________' supports understanding.
- Comparisons of measure can be represented as multiplication equations.
- Division can be represented as multiplication by a unit fraction
Keywords
Times the mass/capacity/volume - Times the mass/capacity/volume is a phrase that is used to compare and describe. For example, one bear might be three times the mass of another bear - it is three times as heavy.
Mass - Mass is a measure of how much matter something contains. It is commonly measured by how much something weighs. Mass can be measured in kilograms and grams.
Capacity - Capacity is a measure of the maximum amount of liquid a container can hold when full. Capacity can be measured in millilitres and litres.
Volume - Volume is the amount of space that an object takes up. In this case, the specific amount of liquid in a container. Volume can be measured in millilitres and litres.
Common misconception
Children may say 'ten times heavier' which is imprecise. Children are more familiar with multiplication resulting in an increase and need to appreciate that it can also result in a decrease.
We say, 'ten times the original mass' because this is more precise, especially when the scale factor is fractional. When we multiply by a unit fraction, it is the same as dividing the whole by the number of equal parts in it, resulting in a decrease.
To help you plan your year 5 maths lesson on: Compare and describe measurements involving mass and capacity, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 5 maths lesson on: Compare and describe measurements involving mass and capacity, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 2 maths lessons from the Compare and describe measurements using knowledge of multiplication and division unit, dive into the full primary maths curriculum, or learn more about lesson planning.

Licence
Prior knowledge starter quiz
6 Questions
Q1.Izzy runs 400 m in 2 minutes. Jacob walks one quarter times the distance in the same time. How far does Jacob walk?
Q2.Izzy runs 400 m in 2 minutes. Jacob walks one quarter times the distance in the same time. How much further does Izzy run than Jacob walks? Izzy runs m further than Jacob.
Q3.Which expression is equal to 150 x $${1}\over{3}$$?
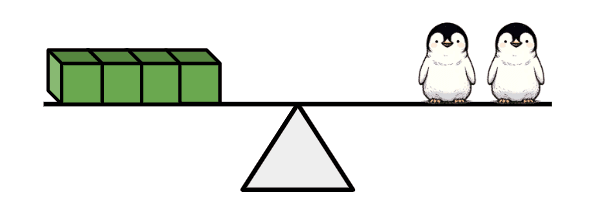
Q4.Which two equations represent the length of the blue bar in this bar model?
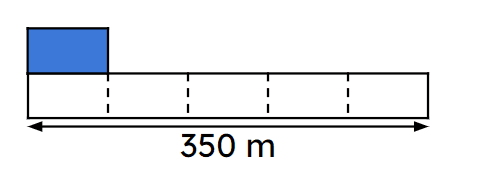
Q5.It is 6 km from home to school. One third of the way to school there is a big tree. How far away is the tree from home? The tree is km away from home.
Q6.Match the equivalent expressions.
120 x $${1}\over{4}$$ -
120 ÷ 4
120 x $${1}\over{3}$$ -
120 ÷ 3
150 x $${1}\over{3}$$ -
150 ÷ 3
120 x $${1}\over{6}$$ -
120 ÷ 6
Assessment exit quiz
6 Questions
Q1.The mass of a bear cub is 30 kg. The mass of the mother bear is three times the mass of the cub. Which bar model represents this?

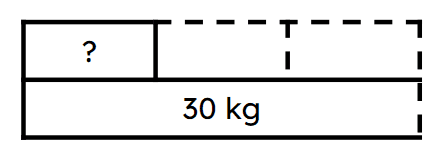
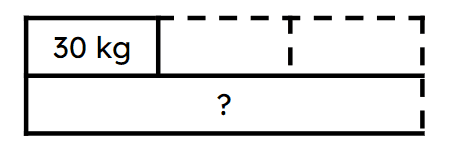
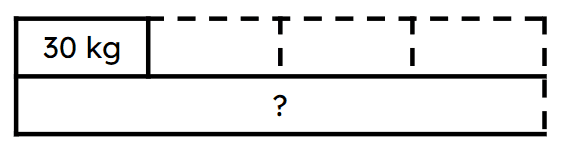
Q2.Look at the bar model. Which equation can be formed from the bar model to calculate the mass of the mother bear if the cub has a mass of 30 kg?
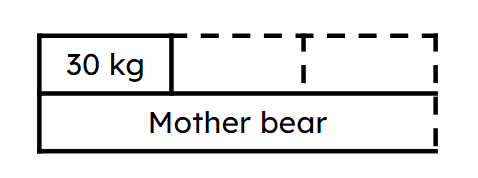
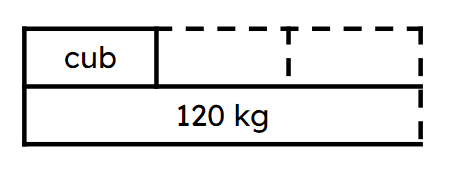
Q3.The mass of the mother bear is 120 kg. Which statement describes the mass of the cub?
Q4.The capacity of a cup is one fifth times the capacity of of a jug. Which bar model represents this statement?
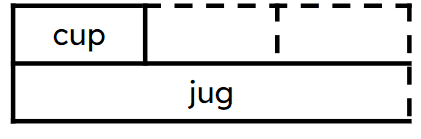
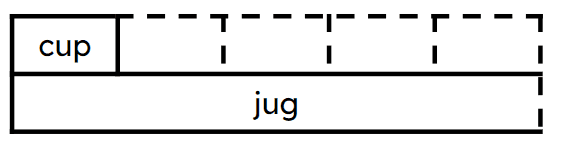
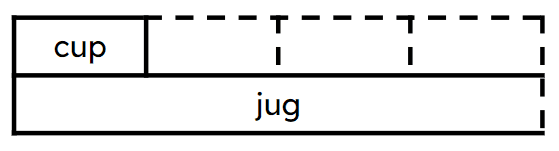
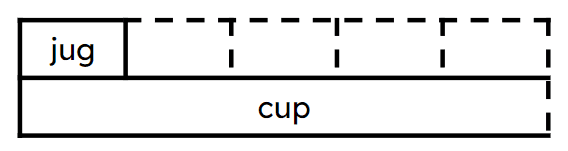
Q5.The capacity of a cup is one fifth times the capacity of of a jug. The capacity of the jug is 1 l 500 ml. The capacity of the cup is ml.
Q6.Which statements describe this image?