Year 9
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- In this lesson, we will explore how we can use quadratic graphs to solve maximum and minimum problems.
Licence
This content is made available by Oak National Academy Limited and its partners and licensed under Oak’s terms & conditions (Collection 1), except where otherwise stated.
5 Questions
Q1.
Select the word that best fills in the gap: Sometimes ___________ can be used to model situations.
expanding
factorisation
mathematical contexts
Q2.
"I think of two numbers with a difference of 3 and multiply them together." Which expression bests represents the statement?
3x
3x + 3
x - 3
Q3.
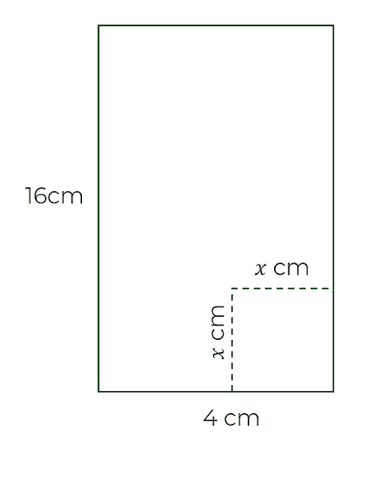
A square is cut out of the rectangle. Give an expression for the area.
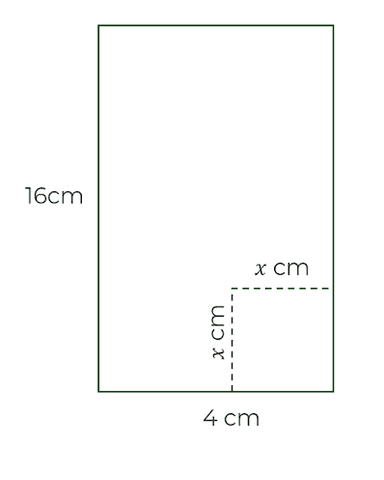

Option 1

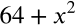
Option 3
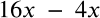
Option 4
Q4.
A square is cut out of the rectangle. What is the maximum area?
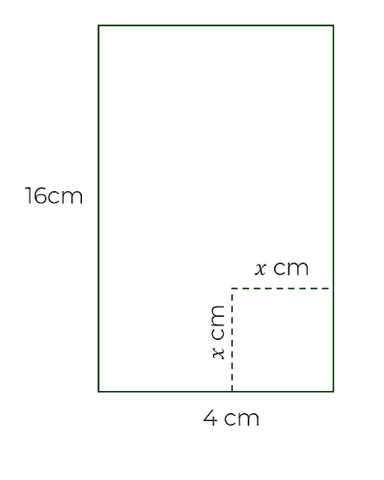
60 cm²
62 cm²
80 cm²
Q5.
A square is cut out of the rectangle. What is the minimum area?
0 cm²
16 cm²
4 cm²
64 cm²
6 Questions
Q1.
The length and width of a rectangle add to 4cm. Stacey thinks only 2 different rectangles are possible. Do you agree?
No, Stacey is incorrect, there is only 1 possible rectangle.
Yes, Stacey is correct.
Q2.
A rectangle's length is 2cm greater than its width. Which expression gives the area?
2x + 4
2x cm²
x² + 2
Q3.
A triangle's height is 4 times greater than its base. Which expression gives the area?
4x²
5x
5x²
Q4.
The length and width of a rectangle add to 14 cm. Which expression gives the area?
14 - x²
14x - 4x²
14x²
Q5.
The length and width of a rectangle add to 14 cm. What is the largest possible area?
14 cm²
196 cm²
40 cm²
56 cm²
Q6.
A triangle has a base and height that sum to 20cm. What is the upper bound of the triangle's area?
10 cm²
100 cm²
There is not an upper bound.

