Skip to content
Oak National Academy
Oak National Academy
View my library
0
Teachers
Pupils
View unit
New
New
Lesson 4 of 18
  • Year 7

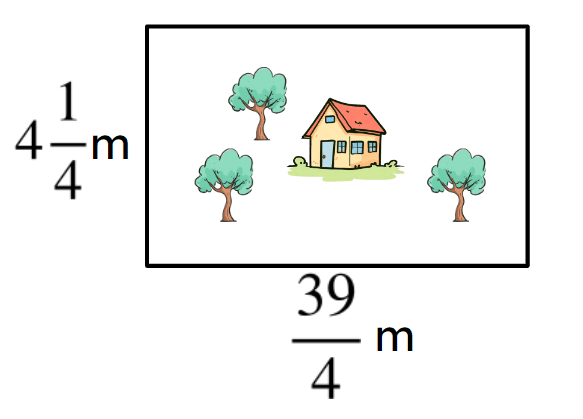
Checking and securing converting mixed numbers to improper fractions

I can use awareness that fractions of the form a/b, where a>b, are greater than one and so convert from mixed numbers to improper fractions.

Download all
View unit
Lesson 4 of 18
New
New
  • Year 7

Checking and securing converting mixed numbers to improper fractions

I can use awareness that fractions of the form a/b, where a>b, are greater than one and so convert from mixed numbers to improper fractions.

Download all

These resources were made for remote use during the pandemic, not classroom teaching.

Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.

View new resources

Lesson details

Key learning points

  1. Fractions where the numerator is greater than the denominator are greater than one.
  2. Whole numbers can be written as improper fractions.
  3. Mixed numbers can be converted into improper fractions.
  4. It may be helpful to switch between mixed number and improper fractions depending on the context.

Keywords

  • Proper fraction - A proper fraction is a fraction where the numerator is less than the denominator.

  • Improper fraction - An improper fraction is a fraction where the numerator is greater than or equal to the denominator.

  • Mixed number - A mixed number is an improper fraction written as its integer part plus the fractional part where the fractional part is a proper fraction.

Common misconception

Some pupils can miscalculate the mixed number to an improper fraction.

For smaller numbers, encourage pupils to draw bar models or diagrams to show the relationship between the whole and the improper fraction.


To help you plan your year 7 maths lesson on: Checking and securing converting mixed numbers to improper fractions, download all teaching resources for free and adapt to suit your pupils' needs...

Ask pupils when have they heard the use of mixed numbers in real life and when have they heard numbers given as an improper fraction. A good discussion point is how we use mixed numbers more but improper fractions are easier to calculate with.
Teacher tip

Licence

This content is © Oak National Academy Limited (2025), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).

Lesson video

Skip lesson video

Loading...

Prior knowledge starter quiz

Download quiz pdf

6 Questions

Q1.
Match together each type of fraction with an example of that fraction.

Correct Answer:mixed number,$$2 \frac {8}{9}$$

$$2 \frac {8}{9}$$

Correct Answer:proper fraction,$$\frac {8}{9}$$

$$\frac {8}{9}$$

Correct Answer:improper fraction,$$\frac {9}{8}$$

$$\frac {9}{8}$$

Q2.
Write the correct symbol (<, > or =) to make the statement true: 236 ÷ 237 1

Correct Answer: <

Q3.
Match each statement to the symbol that should go in the box to make each statement true.

Correct Answer:$$\frac{6}{5} \square 1$$,>

>

Correct Answer:$$\frac{5}{6} \square 1$$,<

<

Correct Answer:$$\frac{6+5}{5+6 } \square 1$$,=

=

Q4.
Aisha writes: $$\frac{17} {6} = \square \frac {5}{6}$$. Jun should write the number in the box.

Correct Answer: 2, two

Q5.
Izzy writes: $$\frac{23} {4} = 5 \frac {\square}{4}$$. Izzy should write the number in the box.

Correct Answer: 3, three

Q6.
Match each improper fraction to its equivalent mixed number.

Correct Answer:$$ \frac {23}{6}$$,$$3 \frac {5}{6}$$

$$3 \frac {5}{6}$$

Correct Answer:$$ \frac {5}{3}$$,$$1 \frac {2}{3}$$

$$1 \frac {2}{3}$$

Correct Answer:$$ \frac {15}{6}$$,$$2 \frac {1}{2}$$

$$2 \frac {1}{2}$$

Correct Answer:$$ \frac {14}{6}$$,$$2 \frac {1}{3}$$

$$2 \frac {1}{3}$$

Correct Answer:$$ \frac {10}{3}$$,$$3 \frac {1}{3}$$

$$3 \frac {1}{3}$$

Assessment exit quiz

Download quiz pdf

6 Questions

Q1.
Fractions where the numerator is greater than or equal to the denominator are called fractions.

Correct Answer: improper, Improper

Q2.
The integer that is equivalent to the fraction $$20 \over 4$$ is .

Correct Answer: 5, five

Q3.
Write $$4\frac{2}{3}$$ as an improper fraction.

$$11\over2$$
Correct answer: $$14\over3$$
$$13\over3$$
$$12\over3$$

Q4.
Write the correct symbol (<, > or =) to make the statement true: $$15 \frac {1}{4} $$ $$\frac {31}{2} $$

Correct Answer: <

Q5.
Starting with the smallest, put these fractions and mixed numbers in order of size.

1 - $$1\frac {2}{9} $$
2 - $$1\frac {1}{3} $$
3 - $$\frac {13}{9} $$
4 - $$1\frac {2}{3} $$
5 - $$2\frac {1}{9} $$
6 - $$\frac {20}{9} $$

Q6.
A gardener puts up a fence around a rectangular garden. Each fence panel is 1 metre long and costs £35. What is the total cost of the fencing? £

An image in a quiz
Correct Answer: 980, £980, 980.00, £980.00