Myths about teaching can hold you back


- Year 8
Problem solving with constructions
I can use my knowledge of constructions to solve problems.


- Year 8
Problem solving with constructions
I can use my knowledge of constructions to solve problems.
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- Shapes made from triangles can be constructed.
- By investigation it is possible to accurately construct multiple polygons.
- Shortest distances can be found using constructions with perpendicular lines.
Keywords
Bisect - To bisect means to cut or divide an object into two equal parts.
Rhombus - A rhombus is a parallelogram where all sides are the same length.
Common misconception
You always need to draw circles that are the same size to construct any polygon.
Some polygons, such as kites, require you to construct two circles of different size, as long as they still intersect at two points.
To help you plan your year 8 maths lesson on: Problem solving with constructions, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 8 maths lesson on: Problem solving with constructions, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 3 maths lessons from the Constructions unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Prior knowledge starter quiz
6 Questions
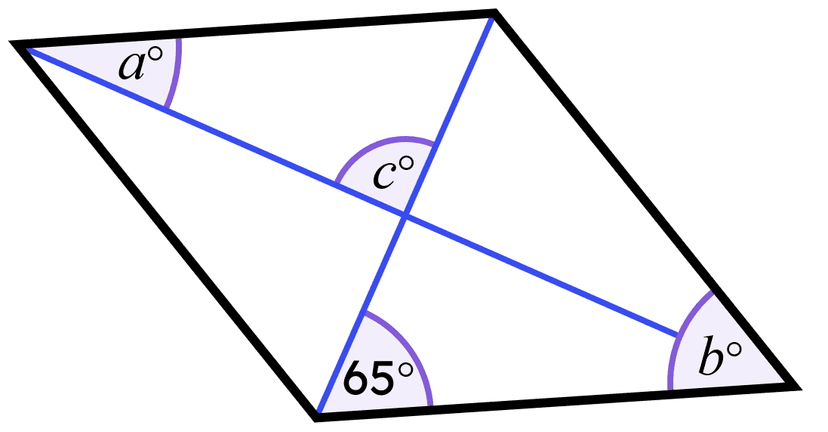
Q1.This quadrilateral is a rhombus. Find the value of $$a+b+c$$.
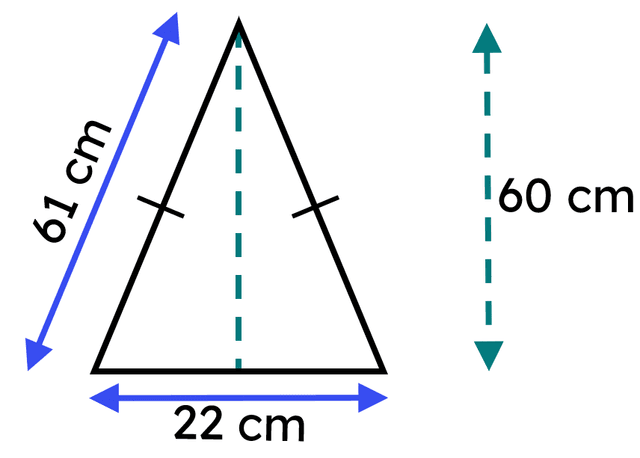
Q2.This triangle is reflected with the line of reflection at its base side. The resultant quadrilateral is a rhombus. What is the area of this rhombus (in cm²)?
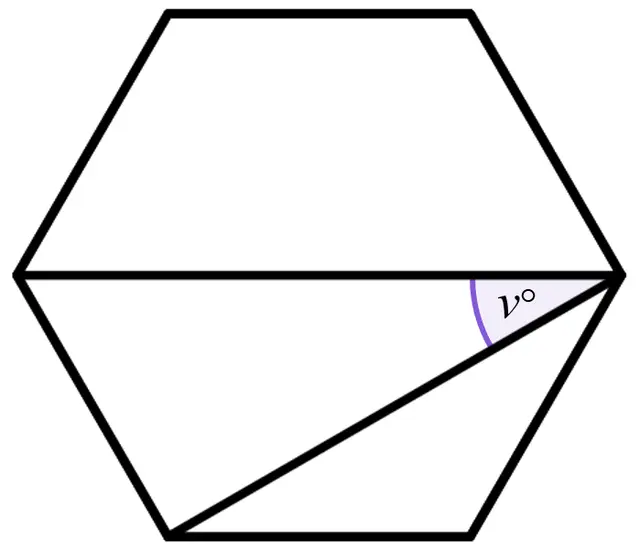
Q3.This hexagon is regular. Find the size of angle $$v$$, in degrees.
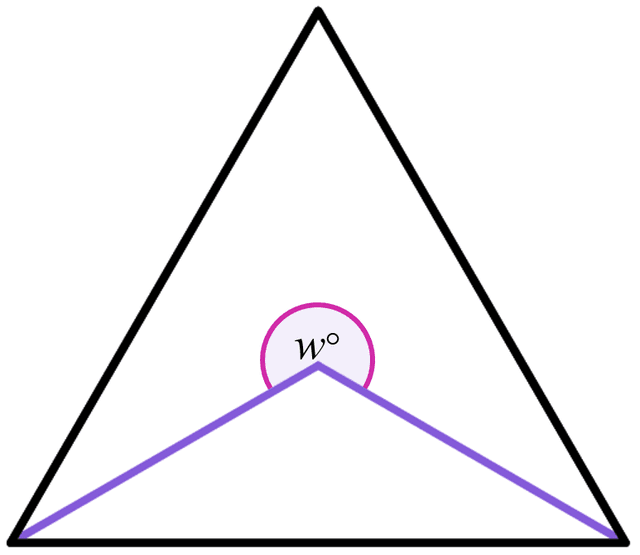
Q4.The triangle is equilateral, with two angle bisectors extending from the bottom two angles of the equilateral triangle and intersecting inside the triangle. Find the size of angle $$w$$.
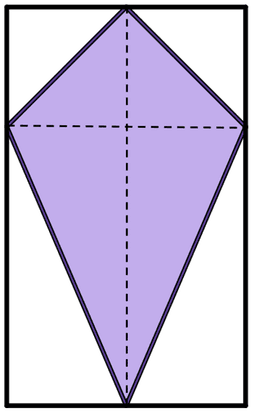
Q5.This diagram shows a kite enclosed by a rectangle. If the rectangle has an area of 780 cm², find the area of the kite, in cm².
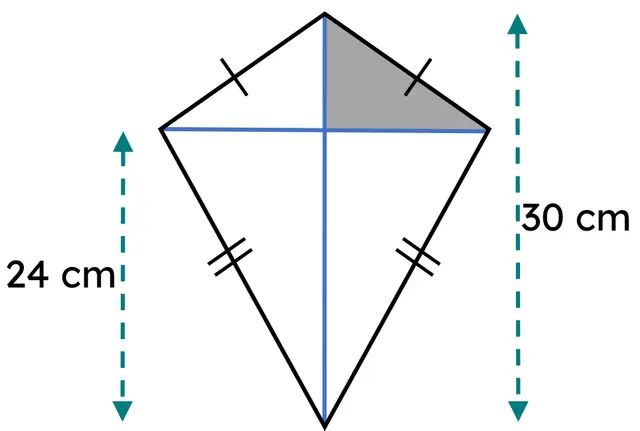
Q6.This kite has an area of 270 cm². What is the area of the shaded region: the right-angled triangle on the top, right of the kite? Give your answer in cm².
Assessment exit quiz
6 Questions
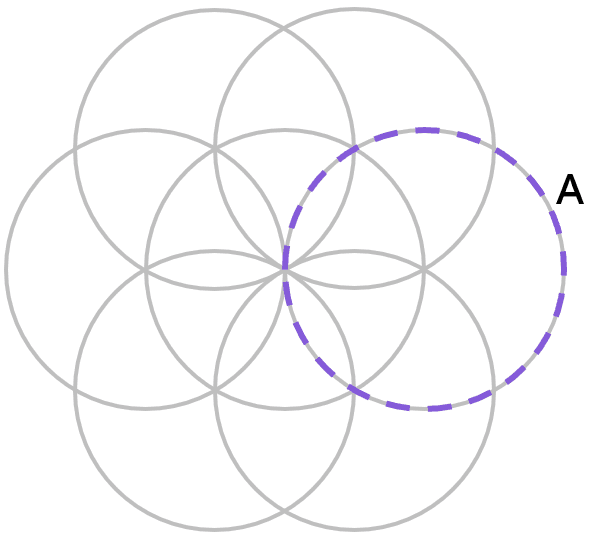
Q1.In this six-petal flower construction, at how many points does circle A intersect with at least one other circle?
Q2.Which of these polygons can be formed by joining up combinations of intersections between any line segment or circle?
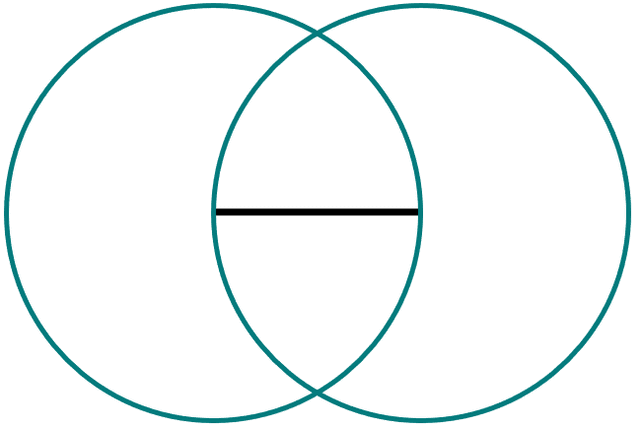
Q3.Which of these polygons can be formed by joining up combinations of intersections between any line segment or circle?
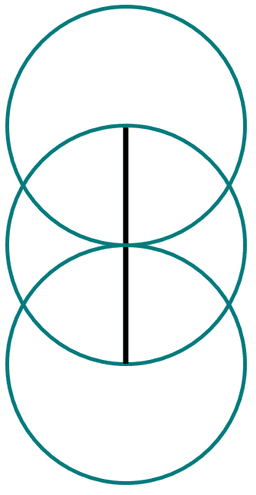
Q4.Which of these statements is true about the construction of a perpendicular bisector?
Q5.Which two pairs of points need to be joined with a line segment to find the fourth point in the kite?
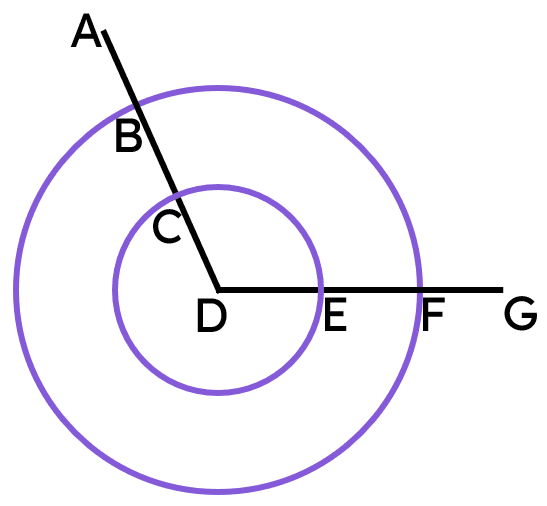
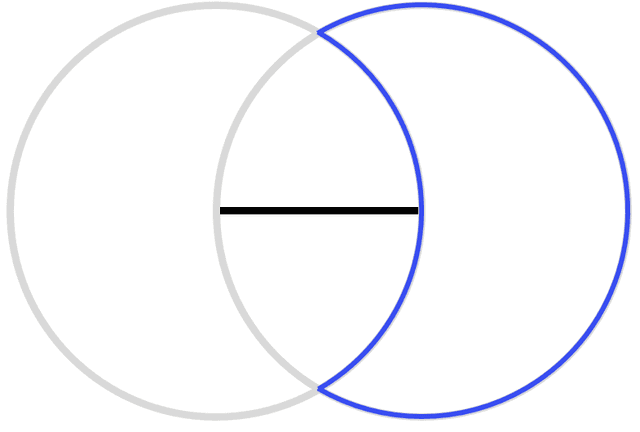
Q6.This "crescent moon" logo can be formed using the construction of an equilateral triangle that uses two congruent circles of radius 9 cm. What is the perimeter of this logo (in cm, rounded to 1 dp)?