Myths about teaching can hold you back


- Year 9
Demonstrating Pythagoras' theorem
I can appreciate there is a relationship between the lengths of the sides of a right-angled triangle.


- Year 9
Demonstrating Pythagoras' theorem
I can appreciate there is a relationship between the lengths of the sides of a right-angled triangle.
Lesson details
Key learning points
- A visual approach can help you understand the structure behind Pythagoras' theorem.
- There is a difference between proof and demonstration.
- A demonstration would be showing Pythagoras' theorem works for specific right-angled triangles.
- A proof is generalised i.e. using four congruent triangles arranged in a particular way inside a square.
- The sum of the squares of the two shorter sides equals the square of the longest side.
Keywords
Pythagoras' theorem - Pythagoras’ theorem shows that the sum of the squares of the two shorter sides of a right-angled triangle is equal to the square of its longest side (the hypotenuse).
Common misconception
Pythagoras' theorem is just a relationship between the three sides of a right-angled triangle.
Whilst this is true, Pythagoras' theorem can more visually be represented as three squares whose sides are equal in length to the three sides of the triangle. The sum of the areas of the two smaller squares is equal to the area of the larger square.
To help you plan your year 9 maths lesson on: Demonstrating Pythagoras' theorem, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 9 maths lesson on: Demonstrating Pythagoras' theorem, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 3 maths lessons from the Geometrical properties: similarity and Pythagoras' theorem unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Equipment
Licence
Prior knowledge starter quiz
6 Questions
Q1.Which of these are square numbers?
Q2.Match each statement to its value.
5 squared -
25
the square of 4 -
16
12² -
144
20 × 20 -
400
$$\sqrt{4}$$ -
2
$$\sqrt{25}$$ -
5
Q3.The difference between 11² and 7² is .
Q4.8² + 6² – 10² = .
Q5.Which of these show a fully and correctly correctly marked square?
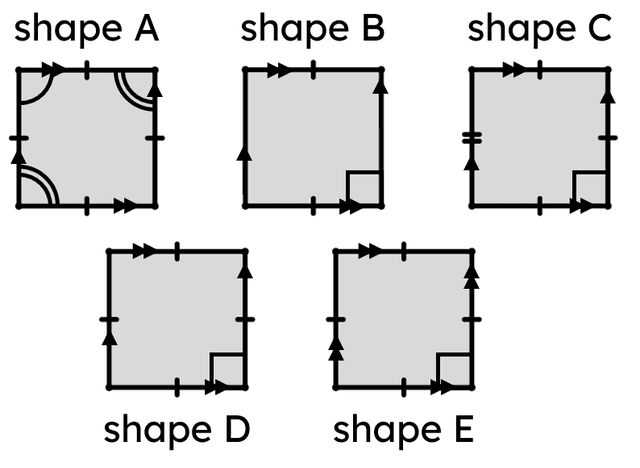
Q6.Starting with the smallest, place these angles in order of size.
Assessment exit quiz
6 Questions
Q1.What is the size of the largest angle in the triangle formed from these three squares?
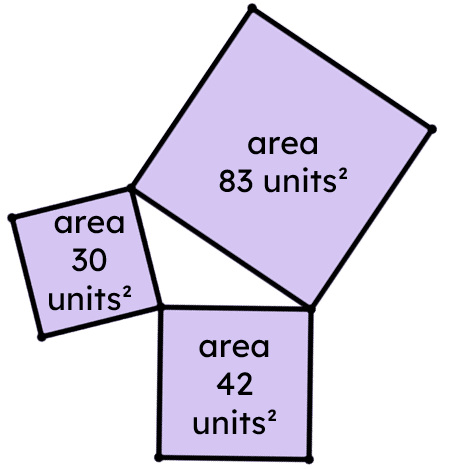
Q2.Which of these three angles is the largest?
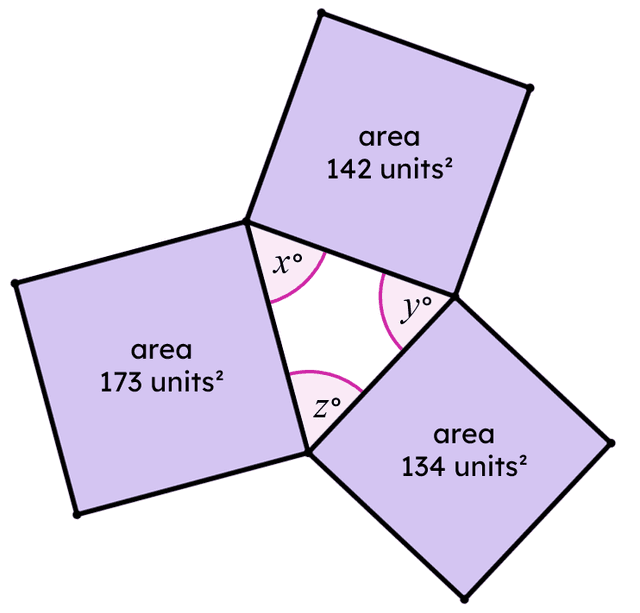
Q3.Which of these are possible sizes for the largest angle?


