Myths about teaching can hold you back
Learn why
New
New
Lesson 4 of 15
- Year 8
Checking and securing plotting a relationship
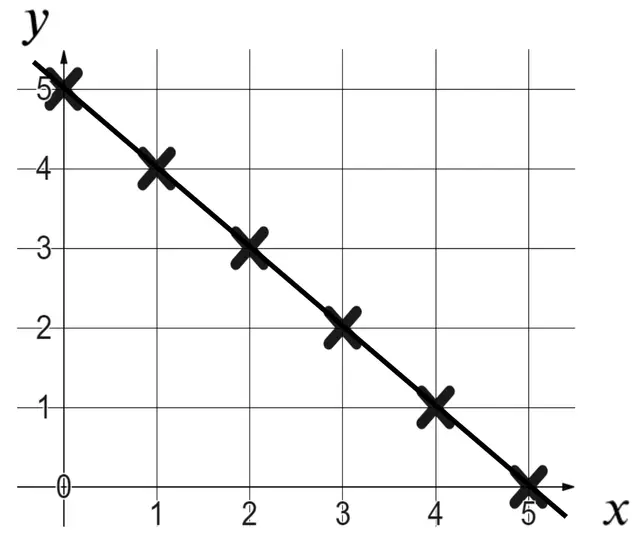
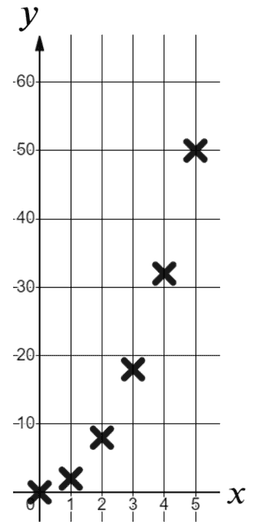
I can use a graphical representation to show all of the points (within a range) that satisfy a relationship.
Lesson 4 of 15
New
New
- Year 8
Checking and securing plotting a relationship
I can use a graphical representation to show all of the points (within a range) that satisfy a relationship.
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
These resources were created for remote use during the pandemic and are not designed for classroom teaching.
Lesson details
Assessment exit quiz
Download quiz pdf