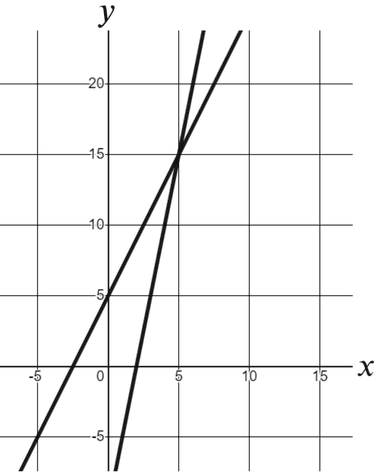
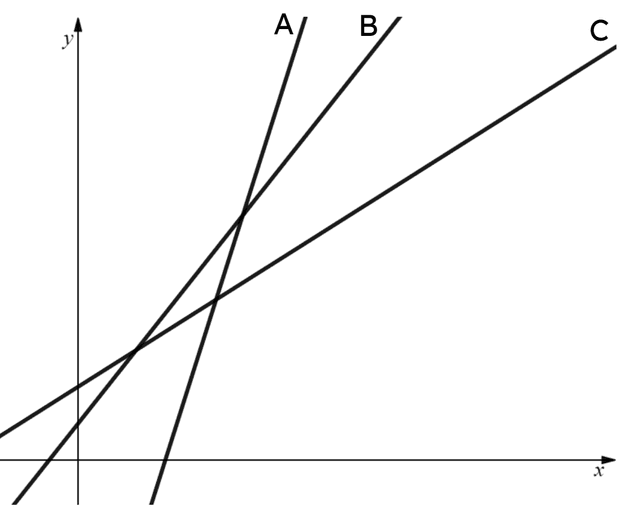
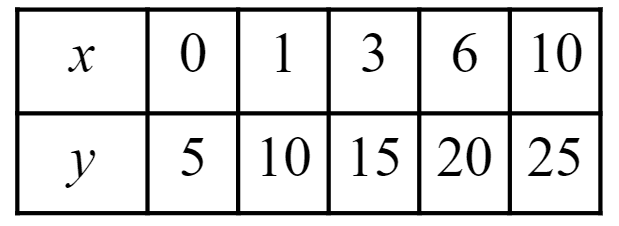
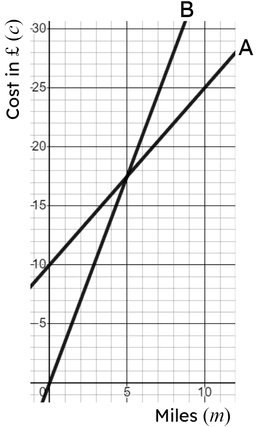
To help you plan your year 8 maths lesson on: Problem solving with graphing linear relationships, download all teaching resources for free and adapt to suit your pupils' needs.

The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.

We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.

The assessment exit quiz will test your pupils' understanding of the key learning points.

Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.

Explore more key stage 3 maths lessons from the Graphical representations of linear equations unit, dive into the full secondary maths curriculum, or learn more about lesson planning.