Skip to content
Oak National Academy
Oak National Academy
Teachers
Pupils
New
New
Year 8

Area of composite shapes

I can solve area problems of composite shapes involving whole and/or part circles.

Download all resources
arrow-right
Share activities with pupils
arrow-right
New
New
Year 8

Area of composite shapes

I can solve area problems of composite shapes involving whole and/or part circles.

Download all resources
arrow-right
Share activities with pupils
arrow-right
warning

These resources will be removed by end of Summer Term 2025.

Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
View new resources
arrow-right

Lesson details

Key learning points

  1. The area parts of a circle can be found using the area formula and reasoning.
  2. The area of shapes made from circles and parts of circles can be found.
  3. The area of composite shapes that include circles can be found.

Keywords

  • Sector - A sector is the region formed between two radii and their connecting arc.

Common misconception

To find the area of a quarter-circle divide the radius by 4 to use as part of the calculation.

You must divide the area by 4, not the radius. The radius gets squared when calculating area so the division of r would be applied twice.

Encourage students to sketch the component parts of each composite shape. This is especially helpful in visualising the shape of both the negative and positive space in a composite shape with a component part removed from the object.
Teacher tip

Licence

This content is © Oak National Academy Limited (2024), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).

Lesson video

Skip lesson video

Loading...

Starter quiz

Download starter quiz

6 Questions

Q1.
What is $${2\over3}$$ of 144 cm?
96
Correct answer: 96 cm
216
216 cm
Q2.
Which of these formulae finds the area of a circle with radius $$r$$?
$$area = {\pi} {\times}r$$
$$area = 2{\times}{\pi} {\times}r$$
$$area = {\pi} {\times}r2$$
Correct answer: $$area = {\pi} {\times}r^2$$
Q3.
Find the area of a circle with radius of 25 cm, giving your answer both in terms of $$\pi$$ and in decimal form, rounded to 1 decimal place.
25$$\pi$$ cm²
50$$\pi$$ cm²
Correct answer: 625$$\pi$$ cm²
1963.4 cm²
Correct answer: 1963.5 cm²
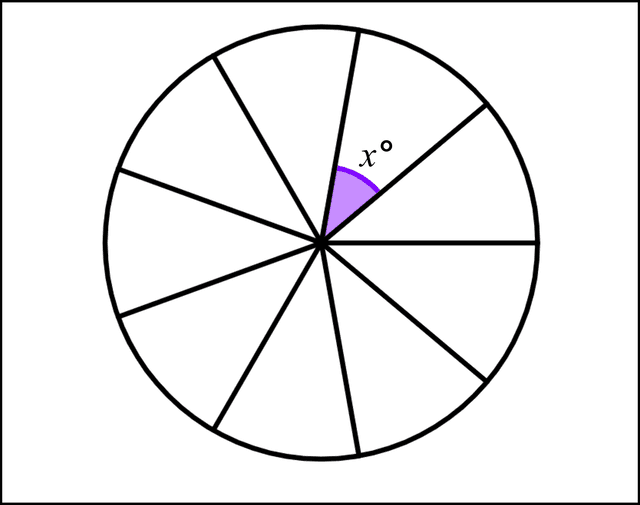
Q4.
From its centre, this circle has been split up into 9 equally-sized sectors. How many degrees is the angle marked x?
An image in a quiz
Correct Answer: 40, 40°, 40degrees, 40 degrees
Q5.
Match each statement to the correct value for a circle with a diameter of 80 units.
Correct Answer:The radius is,40

40

Correct Answer:The area in terms of $$\pi$$,1600$$\pi$$

1600$$\pi$$

Correct Answer:The area in decimal form is,5026.5

5026.5

Correct Answer:The circumference is,80$$\pi$$

80$$\pi$$

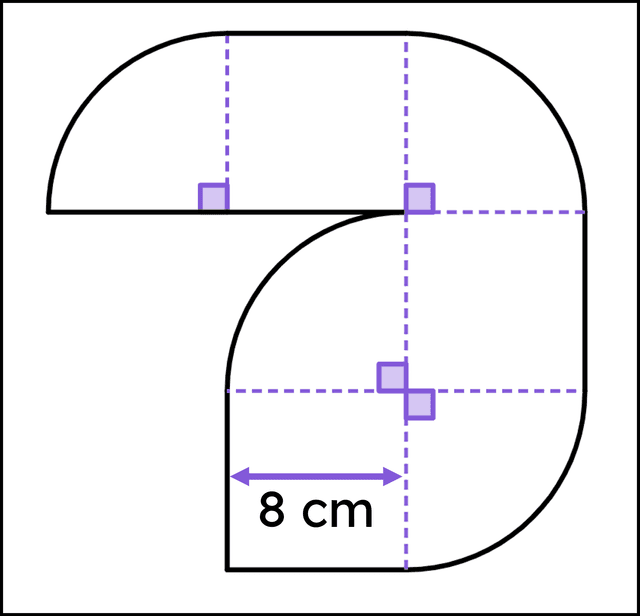
Q6.
Which of these statements is true for this composite shape?
An image in a quiz
$$a$$ = 7 cm
Correct answer: $$a$$ = 15 cm
$$a$$ = 18 cm
Correct answer: The area of the composite shape is 1128 cm².
The area of the composite shape is 1190 cm².

Exit quiz

Download exit quiz

6 Questions

Q1.
A quarter-circular sector is cut out of a circle. The original circle had an area of 120$$\pi$$ cm². What is the area of the quarter-circle?
Correct answer: 30$$\pi$$ cm²
40$$\pi$$ cm²
94.25$$\pi$$ cm²
480$$\pi$$ cm²
Correct answer: 94.25 cm²
Q2.
A sector with a 60° angle is cut out of a circle. The original circle had an area of 3072 inches². The area of the sector is square inches.
Correct Answer: 512, 512 square inches, 512 inches²
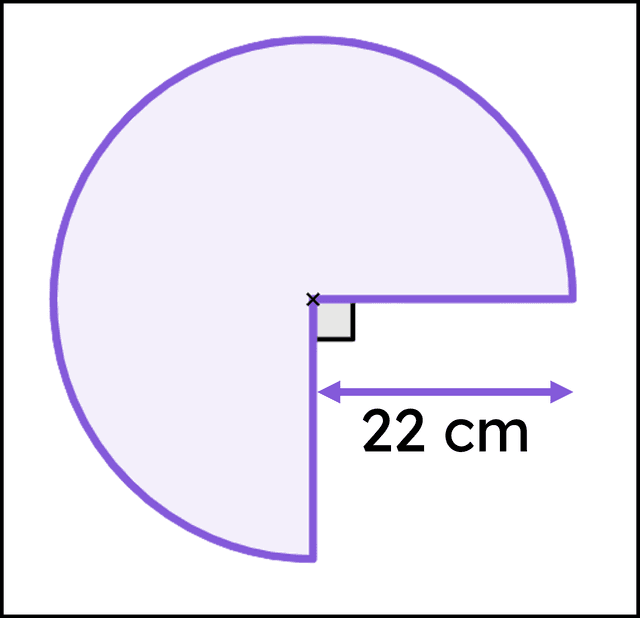
Q3.
Which of the following statements is true for this sector?
An image in a quiz
This sector is $$2\over3$$ the area of a circle that has the same radius.
Correct answer: This sector is $$3\over4$$ the area of a circle that has the same radius.
The area of this sector is 16.5$$\pi$$ cm².
Correct answer: The area of this sector is 363$$\pi$$ cm².
The area of this sector is 484$$\pi$$ cm².
Q4.
This composite shape is broken down into its component parts, made from circular sectors and quadrilaterals. Match each component part and composite shape to its area.
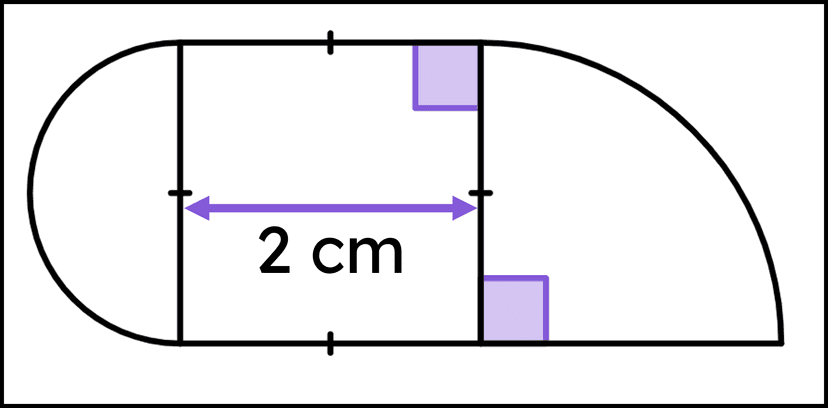
An image in a quiz
Correct Answer:area of square,4 cm²

4 cm²

Correct Answer:area of semicircle,$${1\over2}\pi$$ cm²

$${1\over2}\pi$$ cm²

Correct Answer:area of quarter-circle,3.14 cm²

3.14 cm²

Correct Answer:area of composite shape,8.71 cm²

8.71 cm²

Q5.
Which of these shows the area (written in terms of $$\pi$$) of the shaded region of this composite shape composed of a circular sector and a square?
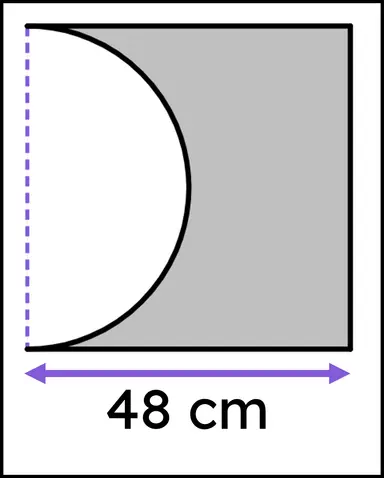
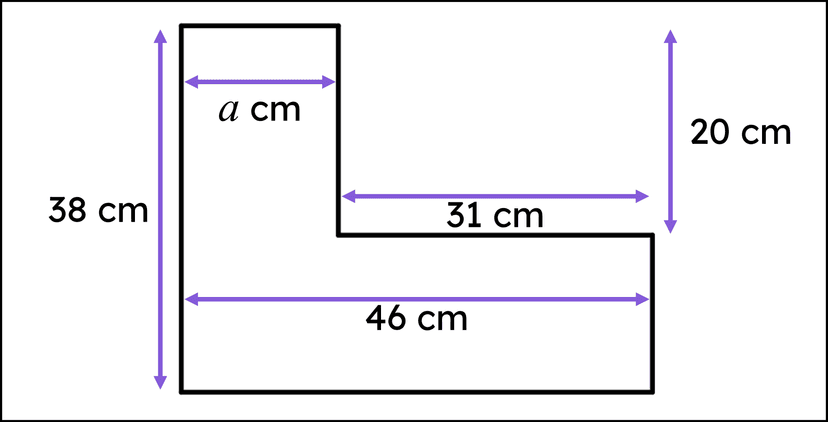
An image in a quiz
2304 cm²
(2304 + 576$$\pi$$) cm²
(2304 + 288$$\pi$$) cm²
(2304 − 576$$\pi$$) cm²
Correct answer: (2304 − 288$$\pi$$) cm²
Q6.
What is the area (in cm²) of this composite shape, composed of only squares and circular sectors, rounded to the nearest integer? cm²
An image in a quiz
Correct Answer: 393, 393 cm², 393cm²