Surface area of prisms
I can find the surface area of 3D shapes in an efficient way.
Surface area of prisms
I can find the surface area of 3D shapes in an efficient way.
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
These resources were created for remote use during the pandemic and are not designed for classroom teaching.
Lesson details
Key learning points
- The surface area of a 3D shape is the sum of the area of all the faces.
- The net of a prism can help find the surface area of a prism but can be time consuming.
- By using known area facts, the area of all the faces can be found and summed.
- It is important to find the surface area systematically and efficiently.
Keywords
Prism - polyhedron with base and identical parallel opposite side with corresponding edges joined by parallelograms.
Faces - Faces are the flat 2D surfaces of a 3D shape.
Nets - The net of a 3D object is a 2D representation of its faces that can be folded up into the 3D object.
Surface area - The surface area is the total area of all the surfaces of a closed 3D shape. The surfaces include all faces and any curved surfaces.
Common misconception
Pupils may try to avoid sketching of nets or faces and in turn miss information.
Reassure pupils that a sketch does not need to be perfect and just needs to convey the key information.
To help you plan your year 8 maths lesson on: Surface area of prisms, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 8 maths lesson on: Surface area of prisms, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 3 maths lessons from the Perimeter, area and volume unit, dive into the full secondary maths curriculum, or learn more about lesson planning.
Licence
Lesson video
Loading...
Prior knowledge starter quiz
6 Questions
Q1.The area of a rectangle with a width of 7 cm and a length of 12 m is m².
Q2.The area of a triangle with a base length of 14 cm and a perpendicular height of 8 cm is cm².
Q3.The area of a trapezium is being calculated $${\text {Area}}={{1}\over{2}} \times {(6+16)} \times {12} = 132 \text{ cm}^2$$. What is the perpendicular height of this trapezium?
Q4.A prism is a polyhedron with a base that is a and a parallel opposite face that is identical. The corresponding edges of the two polygons are joined by parallelograms.
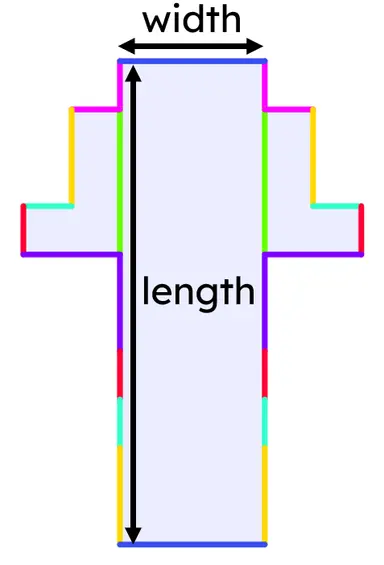
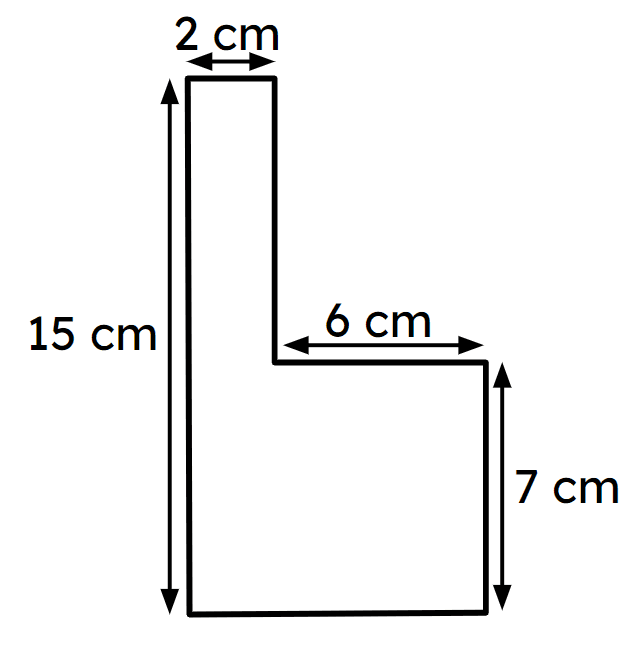
Q5.The perimeter of this shape is cm.
Q6.Match the shape of the base with the name of the prism.
rectangular base -
cuboid
square base -
cube
pentagonal base -
pentagonal prism
triangular base -
triangular prism
Assessment exit quiz
6 Questions
Q1.The surface area is the area of all the surfaces of a closed 3D shape. The surfaces include all faces and any curved surfaces.
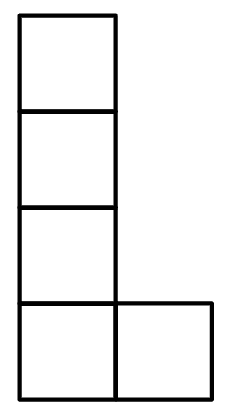
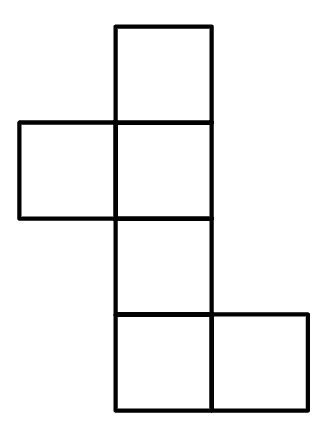
Q2.Which of these are nets for a cube?
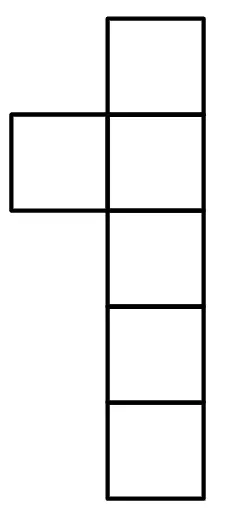
Q3.Here is a right prism. Which of these descriptions is correct?
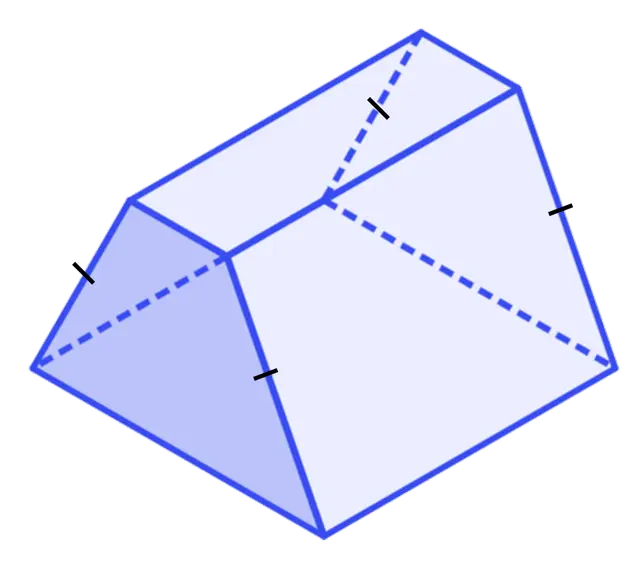
Q4.The areas of the faces of a triangular prism are $$24\text{ cm}^2,24\text{ cm}^2,50\text{ cm}^2, 40\text{ cm}^2\text{ and }30\text{ cm}^2$$ respectively. The surface area is $$\text{ cm}^2$$.
Q5.The surface area of this right-angled isosceles triangular prism is $$\text{ cm}^2$$.
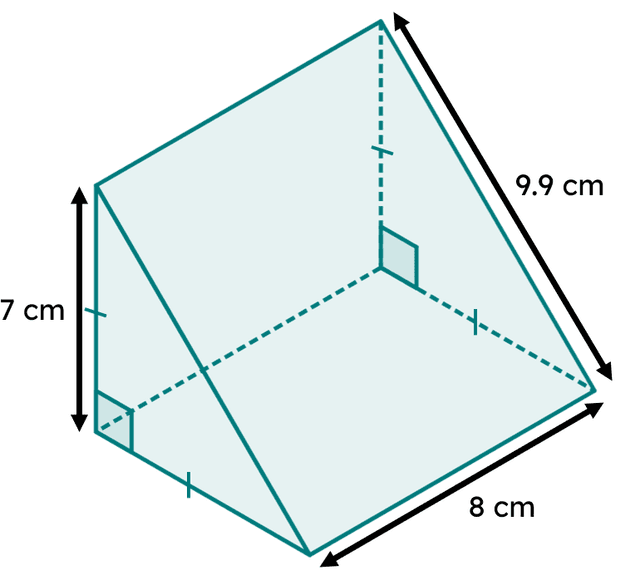
Q6.In a right prism, the rectangular faces can be seen as one large rectangle. The dimensions of the large rectangle are the of the base by the length of the prism.
