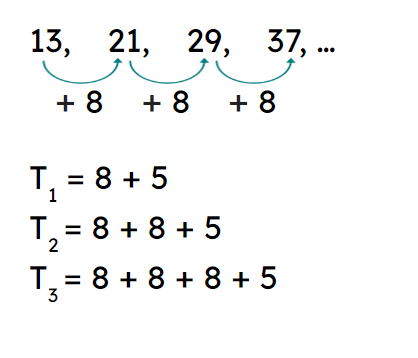New
New
Year 8
Generating a sequence using a position-to-term rule
I can appreciate that a sequence can be generated and described by a position-to-term rule.
New
New
Year 8
Generating a sequence using a position-to-term rule
I can appreciate that a sequence can be generated and described by a position-to-term rule.
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- The position of a term in the sequence is its term number.
- The general term can be used to identify a specific term.
- The general term can be used to generate a sequence .
- The general term can be used to generate any number in the sequence.
- The general term can be used to describe a sequence.
Keywords
Position-to-term - A position-to-term rule describes how to generate the term from the term number.
Common misconception
The position-to-term rule is the initial term add the common difference.
Once pupils have found the additive pattern get them to write each term as a value add the difference.
To introduce this lesson, you could give pupils some numbers that form an additive sequence eg 10, 15, 20, 25 and challenge them to write the numbers as repeated addition of 5. They could do this using cuisenaire rods.
Teacher tip
Licence
This content is © Oak National Academy Limited (2024), licensed on
Open Government Licence version 3.0
except where otherwise stated. See Oak's terms & conditions (Collection 2).Lesson video
Loading...
Starter quiz
Download starter quiz
6 Questions
Q1.
A term-to term rule describes how to calculate the next term from....
the constant additive rule
the multiplier
Correct answer: the previous term
the previous term
the term number
Q2.
True or false. In the sequence 0, 1, 2, 3, 4, ... the 2nd term is 3.
True- the third number is '2'
Correct answer: False- The second number is not '3'
False- The second number is not '3'
There is no way of knowing without the term-to-term rule
Q3.
If the 7 times table start with $$1\times 7 = 7$$ what is the 100th number in the 7 times table?
Correct Answer: 700
700
Q4.
Here are the first 3 terms in a pictorial sequence. Which of these rules could refer to the number of lines in each term?
add 2 to the previous term to get the next term
Correct answer: add 3 to the previous term to get the next term
add 3 to the previous term to get the next term
add 5 to the previous term to get the next term
Correct answer: there are 3 lines per section plus 2 for the base.
there are 3 lines per section plus 2 for the base.
there are 5 lines per section
Q5.
Which of these is an advantage for using a term-to-term rule
Correct answer: They are easy to use to find the next term in a sequence
They are easy to use to find the next term in a sequence
They are easy to use to find any term in a sequence
Correct answer: They work for all sequences where there is a rule between successive terms
They work for all sequences where there is a rule between successive terms
They are unique, the same rule will always produce the same sequence.
There is only one term-to-term rule that will work if you know the first 3 term.
Q6.
Match the sequences with the term-to-term rules.
Correct Answer:-2, -6, -18, -54, ...,multiply the previous term by 3
-2, -6, -18, -54, ... -
multiply the previous term by 3
Correct Answer:-2, -6, -10, -14, ...,add $$-4$$ to the previous term
-2, -6, -10, -14, ... -
add $$-4$$ to the previous term
Correct Answer:-2, -6, -14, -30, ...,multiply the previous term by 2 then subtract 2
-2, -6, -14, -30, ... -
multiply the previous term by 2 then subtract 2
Correct Answer:-2, -6, -12, -20, ...,add $$-4$$, add $$-6$$, add $$-8$$, ...
-2, -6, -12, -20, ... -
add $$-4$$, add $$-6$$, add $$-8$$, ...
Correct Answer:-2, -6, -14, -26, ...,add $$-4$$, add $$-8$$, add $$-12$$, ...
-2, -6, -14, -26, ... -
add $$-4$$, add $$-8$$, add $$-12$$, ...
Correct Answer:-2, -6, -8, -8, ...,add $$-4$$, add $$-2$$, add 0, ...
-2, -6, -8, -8, ... -
add $$-4$$, add $$-2$$, add 0, ...
Exit quiz
Download exit quiz
6 Questions
Q1.
Match up the keywords to their definitions
Correct Answer:term,each value or pattern in a sequence
term -
each value or pattern in a sequence
Correct Answer:term-to-term rule,describes how to get from one term to the next
term-to-term rule -
describes how to get from one term to the next
Correct Answer:position-to-term rule,describes how to calculate the term from the term number
position-to-term rule -
describes how to calculate the term from the term number
Correct Answer:sequence ,a succession of values or patterns usually following a rule.
sequence -
a succession of values or patterns usually following a rule.
Q2.
Using the table shown, match the notation to the term.
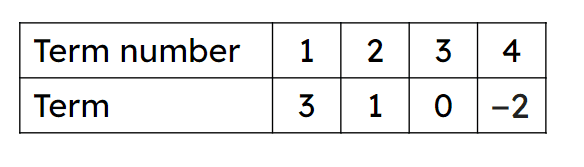
Correct Answer:$$T_1$$,3
$$T_1$$ -
3
Correct Answer:$$T_2$$,1
$$T_2$$ -
1
Correct Answer:$$T_3$$,0
$$T_3$$ -
0
Correct Answer:$$T_4$$,-2
$$T_4$$ -
-2
Q3.
The position-to-term rule for a sequence is 'multiply the term number by 5 then subtract 10'. What is the 20th term in this sequence?
Correct Answer: 90
90
Q4.
Which of these is a position-to-term rule for the number of dots in each pattern of this sequence?
add 6 to the previous term
Correct answer: multiply the term number by 6 then add 4
multiply the term number by 6 then add 4
multiply the term number by 6 then add 10
Multiply the term number by 10
Multiply the term number by 10 then subtract 4
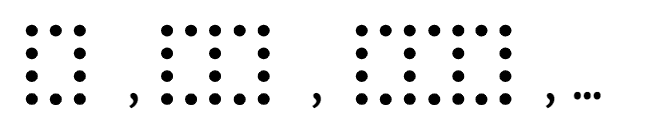
Q5.
Which of these is a position-to-term rule for the sequence 12, 22, 32, 42, 52, ....
the term number add 10
multiply the term number by 10
Correct answer: multiply the term number by 10 then add 2
multiply the term number by 10 then add 2
multiply the term number by 12
multiply the term number by 12 and subtract 2
Q6.
Work out the 100th term in the constant additive sequence which starts: 13, 21, 29, 37, ... The first few lines of working are shown.
Correct Answer: 805
805