Myths about teaching can hold you back


- Year 10•
- Foundation


- Year 10•
- Foundation
Multiple transformations
I can carry out multiple transformations on a shape.
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- A shape can be transformed more than once.
- The first transformation is performed on the object.
- The second transformation is performed on the image.
- The third transformation is performed on the new image etc.
Keywords
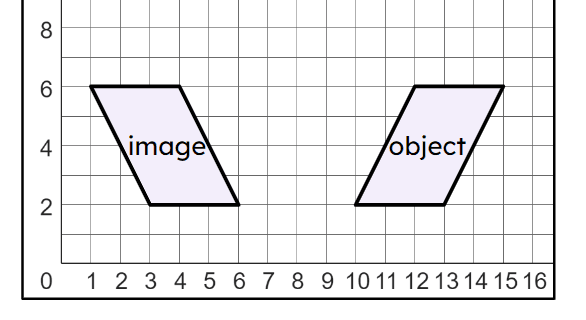
Object - The object is the starting figure before a transformation has been applied.
Image - The image is the resulting figure after a transformation has been applied.
Vector - A vector can be used to describe a translation.
Polygon - A polygon is a flat (2D), closed figure made up of straight line segments.
Common misconception
The number of spaces to translate a shape can be worked out by counting the squares on the grid.
If there are axes, then it is important to check the scales. The length of one square does not always represent one unit.
To help you plan your year 10 maths lesson on: Multiple transformations, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 10 maths lesson on: Multiple transformations, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 4 maths lessons from the Further transformations unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Prior knowledge starter quiz
6 Questions
Q1.The is the starting figure before a transformation has been applied.
Q2.Match each description to the correct vector.
1 left and 2 down -
$$\begin{pmatrix} -1 \\ -2 \\ \end{pmatrix}$$
1 right and 2 up -
$$\begin{pmatrix} 1 \\ 2 \\ \end{pmatrix}$$
2 right and 1 up -
$$\begin{pmatrix} 2 \\ 1 \\ \end{pmatrix}$$
2 right and 1 down -
$$\begin{pmatrix} 2 \\ -1 \\ \end{pmatrix}$$
2 left and 1 up -
$$\begin{pmatrix} -2\\ 1 \\ \end{pmatrix}$$
1 right and 2 up -
$$\begin{pmatrix} 1 \\ 2 \\ \end{pmatrix}$$
Q3.The object has been transformed into the image. The type of transformation shown by the diagram is a .
Q4.Which of these diagrams show a rotation?

Q5.Shape c has been rotated 90° anti-clockwise about (-2, 2). The image is shape .
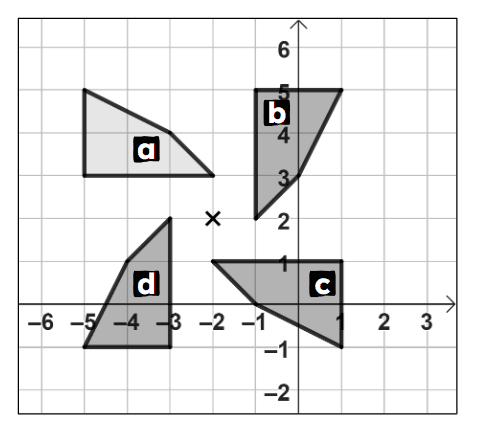
Q6.The point P has coordinates (-2, 3). P is reflected in different lines of reflection. Match the coordinates of the image of P to the equation of the line of reflection.
P'(-2, -3) -
$$x= 0$$
P'(2, 3) -
$$y = 0$$
P'(-3, 2) -
$$y=-x$$
P'(3, -2) -
$$y=x$$
Assessment exit quiz
6 Questions
Q1.A can be used to describe a translation.
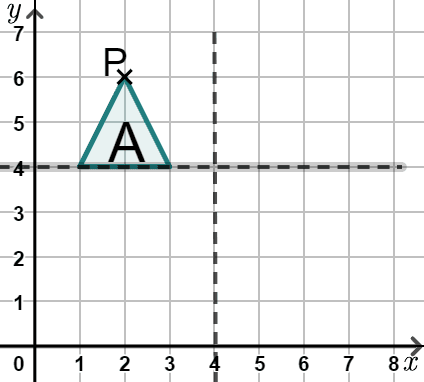
Q2.Aisha reflects shape A in the line $$y=4$$ to A'. She then reflects A' in the line $$x=4$$ to A''. Select the coordinates of P' and P''.
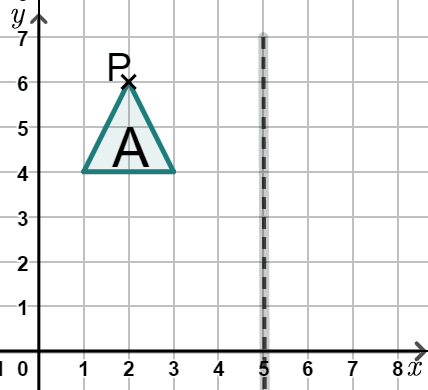
Q3.Jun translates shape A by $$\begin{pmatrix} 2 \\ -1 \\ \end{pmatrix}$$ to A'. He then reflects A' in the line $$x=5$$ to A''. Select the coordinates of P' and P''.
Q4.Sam is using technology to transform some shapes. Sam wants to use Desmos to rotate a shape 90° clockwise. Which of these angles should Sam type into Desmos?
Q5.Here are some buttons that you can use in Desmos for transformations. Match each button to its function.
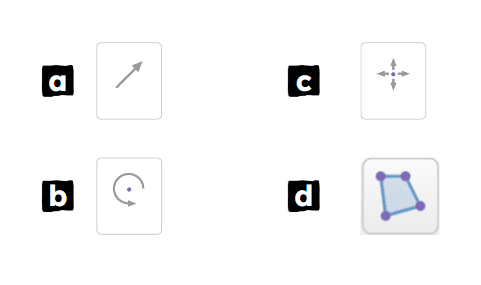
Button a -
translates object
Button b -
rotates object
Button c -
enlarges (dilates) object
Button d -
creates a polygon
Q6.Match each transformation to its description.
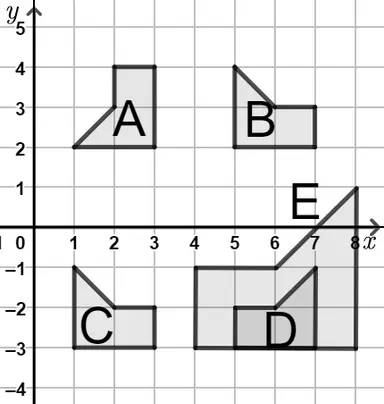
Shape A to shape B -
Rotation $$90$$° clockwise about $$(4, 1)$$
Shape B to shape C -
Translation by $$\begin{pmatrix} -4 \\ -5 \\ \end{pmatrix}$$
Shape C to shape D -
Reflection in the line $$x=4$$
Shape D to shape E -
Enlargement, scale factor $$2$$, about $$(6,-3)$$

