Checking and securing understanding of drawing distance-time graphs
I can draw a distance-time graph to model a journey.


Checking and securing understanding of drawing distance-time graphs
I can draw a distance-time graph to model a journey.
These resources will be removed by end of Summer Term 2025.
Lesson details
Key learning points
- You can sketch a graph based on the information you have been given.
- Important given values should be marked on your sketch.
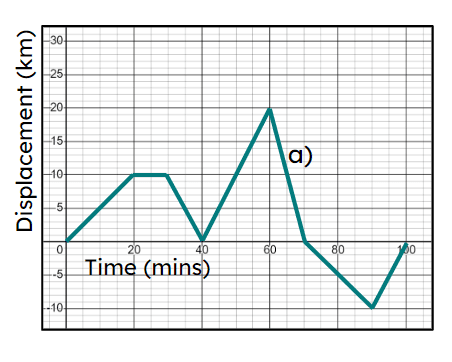
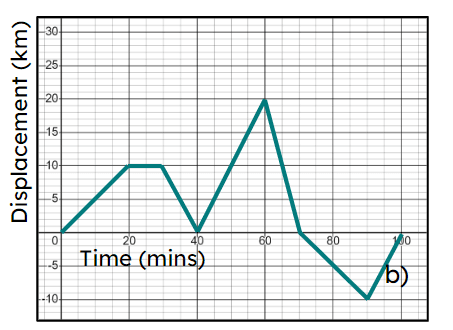
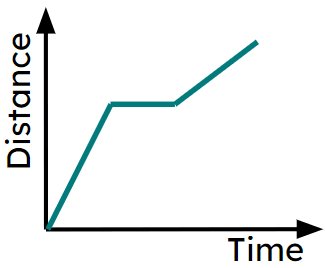
- On a distance-time graph, a horizontal line means no distance was travelled for that time.
- A slanted line means that the distance from the start is changing over time.
Keywords
Displacement - Displacement is the distance from the starting point when measured in a straight line.
Common misconception
Leaving out key information when sketching graphs.
Although sketches do not need to be to scale they do need to contain all key information. Getting pupils to write these on as coordinate pairs is the clearest way. Sketches still have to be useful for the purpose of a model.
To help you plan your year 11 maths lesson on: Checking and securing understanding of drawing distance-time graphs, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 11 maths lesson on: Checking and securing understanding of drawing distance-time graphs, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 4 maths lessons from the Real-life graphs unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Starter quiz
6 Questions
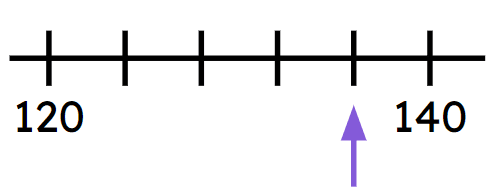
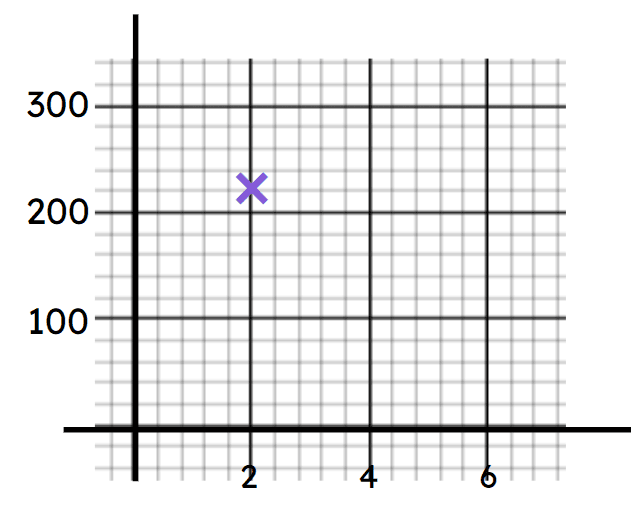
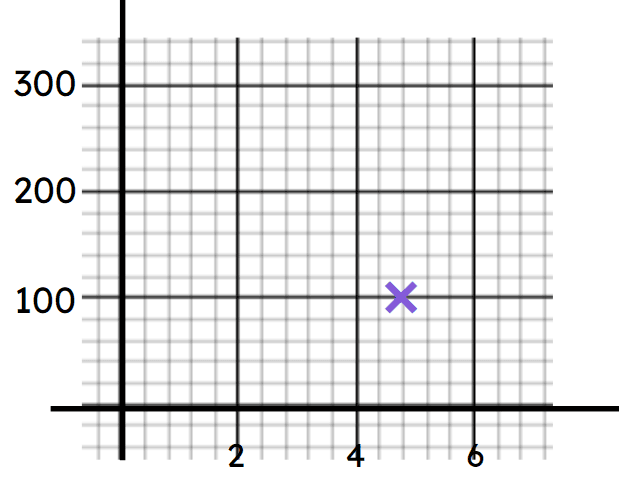
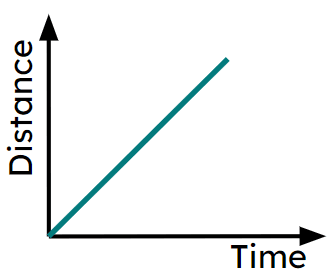
Exit quiz
6 Questions