New

Year 11

Higher

Advanced problem solving with further surface area and volume

I can use my enhanced knowledge of surface area and volume to solve problems.

Download all resources

Share activities with pupils

Link copied to clipboard

New

Year 11

Higher

Advanced problem solving with further surface area and volume

I can use my enhanced knowledge of surface area and volume to solve problems.

Download all resources

Share activities with pupils

Link copied to clipboard

These resources will be removed by end of Summer Term 2025.

Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.

These resources were created for remote use during the pandemic and are not designed for classroom teaching.

View new resources

Slide deck

Download slide deck

Skip slide deck

Lesson details

Key learning points

The surface area of any solid can be calculated by a known method.
The volume of any solid can be calculated by a known method.
Writing an algebraic statement about surface area/volume can be done from a diagram.

Keywords

Volume - The volume is the amount of space occupied by a closed 3D shape.
Surface area - The surface area is the total area of all the surfaces of a closed 3D shape. The surfaces include all faces and any curved surfaces.
Compound shape - A compound shape is a shape created using two or more basic shapes. A composite shape is an alternative for compound shape.

Common misconception

When questions are in context, the length may be described as the depth or height and this can cause some pupils to struggle if they have learned a formula with a particular word.

Remind pupils that the volume of a 3D shape comes from the area of a cross section multiplied by the height or depth. They may need to evaluate a perpendicular length from other given information, using trigonometry or Pythagoras' theorem.

To help you plan your year 11 maths lesson on: Advanced problem solving with further surface area and volume, download all teaching resources for free and adapt to suit your pupils' needs...

Encourage pupils to use exact values throughout their calculation, and only round their answers at the end to ensure the greatest accuracy.

Teacher tip

Equipment

Licence

This content is © Oak National Academy Limited (2025), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).

Lesson video

Skip lesson video

Worksheet

Download worksheet

Skip worksheet

Starter quiz

Download starter quiz

6 Questions

Q1.

Match each measurement to the correct formula.

Correct Answer:Volume of hemisphere,

\frac{2}{3} π r^{3}

$\frac{2}{3} π r^{3}$

Correct Answer:Volume of cone,

\frac{1}{3} π r^{2} h

$\frac{1}{3} π r^{2} h$

Correct Answer:Volume of cylinder,

π r^{2} h

$π r^{2} h$

Correct Answer:Volume of pyramid,

\frac{1}{3} \times area of base \times height

$\frac{1}{3} \times area of base \times height$

Correct Answer:Volume of sphere,

\frac{4}{3} π r^{3}

$\frac{4}{3} π r^{3}$

Q2.

Select the algebraic expression for the volume of this cone.

4 π x^{2}

12 π x^{2}

Correct answer:

48 π x

144 π x

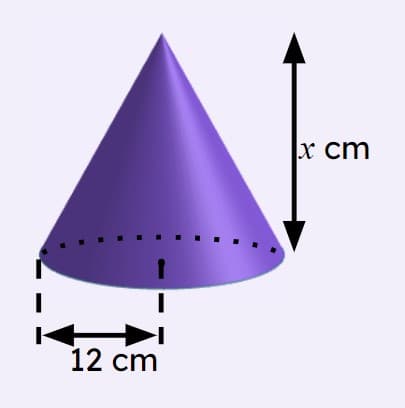
Q3.

The volume of this cone is the same as the volume of a sphere with a radius of 12 cm. The height,

x

of the cone is cm.

Correct Answer: 48

Q4.

Find the surface area of a cube with a volume of 512 cm².

150 cm²

216 cm²

294 cm²

Correct answer: 384 cm²

486 cm²

Q5.

The height,

h

, of a cone is three times the length of its radius. Find an algebraic expression for the volume of the cone in terms of

h

Correct answer:

\frac{1}{27} π h^{3}

\frac{1}{9} π h^{3}

\frac{1}{3} π h^{3}

π h^{3}

3 π h^{3}

Q6.

The radius of a cylinder is half of the height of the cylinder. The volume of the cylinder is 1024𝜋 cm³. The surface area of the cylinder, in terms of 𝜋, is cm².

Correct Answer: 384

Exit quiz

Download exit quiz

6 Questions

Q1.

Match each measurement to the correct formula.

Correct Answer:Surface area of a sphere,

2 π r^{2}

$2 π r^{2}$

Correct Answer:Volume of cylinder,

π r^{2} h

$π r^{2} h$

Correct Answer:Area of curved surface of cone ,

π r l

$π r l$

Correct Answer:Volume of sphere,

\frac{4}{3} π r^{3}

$\frac{4}{3} π r^{3}$

Correct Answer:Curved surface area of cylinder,

2 π r h

$2 π r h$

Correct Answer:Volume of cone,

\frac{1}{3} π r^{2} h

$\frac{1}{3} π r^{2} h$

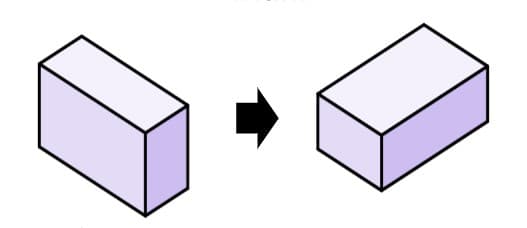
Q2.

The diagram shows a cuboid juice carton which is partially filled with juice. Laura changes the orientation of the carton. Which statement is true?

Correct answer: The height of the juice will be lower.

The height of the juice will rise.

The height of the juice will remain the same.

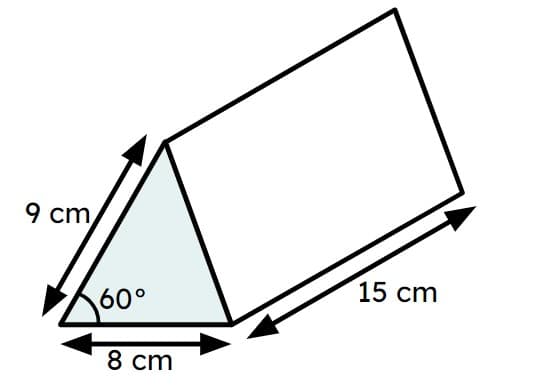
Q3.

Calculate the volume of this prism.

270 cm³ (3 s.f.)

Correct answer: 468 cm³ (3 s.f.)

540 cm³ (3 s.f.)

935 cm³ (3 s.f.)

Q4.

The diagram shows a cuboid. The length of the base is 2 cm greater than the height. Find an expression for the volume of the cuboid.

Correct answer:

6 x (x + 2)

2 x (x + 6)

6 x^{2} + 2

6 x^{2} + 12

Correct answer:

6 x^{2} + 12 x

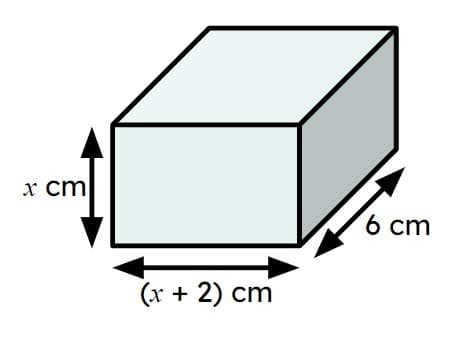
Q5.

The diagram shows a cuboid. The length of the base is 2 cm greater than the height. The volume of the cuboid is 90 cm³. The surface area of the cuboid is

x

is cm².

Correct Answer: 126

Q6.

The volume of the cone is 144𝜋 cm³. Its height is twice the length of its radius. The total surface area of the cone, in terms of 𝜋, is .

144 π

cm²

(36 \sqrt{5}) π

cm²

Correct answer:

(36 + 36 \sqrt{5}) π

cm²

(36 + 36 \sqrt{2}) π

cm²

Advanced problem solving with further surface area and volume

Link copied to clipboard

Advanced problem solving with further surface area and volume

Link copied to clipboard

These resources will be removed by end of Summer Term 2025.

Slide deck

Lesson details

Key learning points

Keywords

Common misconception

How to plan a lesson using our resources

Equipment

Licence

Lesson video

Worksheet

Starter quiz

6 Questions

Exit quiz

6 Questions