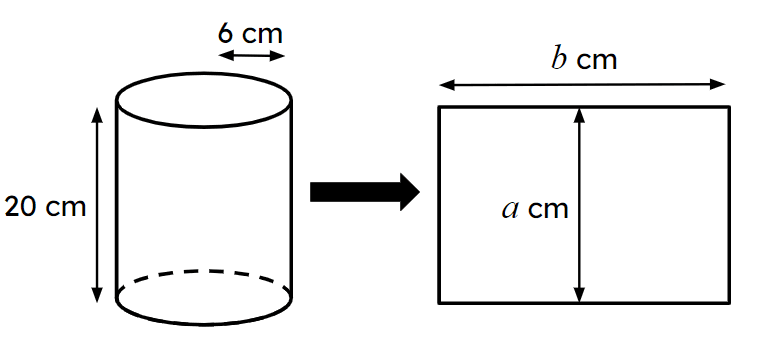
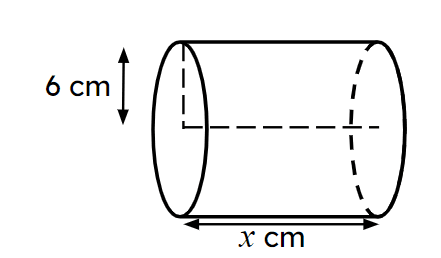
Checking and securing understanding of surface area of a cylinder
I can efficiently calculate the surface area of a cylinder.


Checking and securing understanding of surface area of a cylinder
I can efficiently calculate the surface area of a cylinder.
These resources will be removed by end of Summer Term 2025.
Lesson details
Key learning points
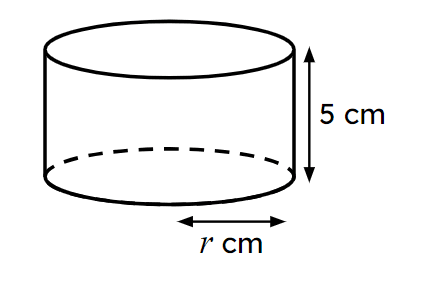
- Drawing the net of a cylinder helps deduce the formula for the surface area.
- The formula can be used to find the surface area of any cylinder.
- Unknown lengths can be found when the surface area is known.
Keywords
Cylinder - A cylinder is a 3D shape with a base that is a circle and a parallel opposite face that is identical. A cross-section of a cylinder made parallel to the base will be congruent to the base.
Surface area - The surface area is the total area of all the surfaces of a closed 3D shape. The surfaces include all faces and any curved surfaces.
Common misconception
Pupils can make errors if given the dimensions/measurements of the cylinder using different units (for example the radius is given in cm and the length in m).
Remind pupils to convert all measurements to the same unit (such as cm or m) before starting the calculation. Usually there is a prompt in the question to use as a guide, for example give your answer in square centimetres.
To help you plan your year 11 maths lesson on: Checking and securing understanding of surface area of a cylinder, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 11 maths lesson on: Checking and securing understanding of surface area of a cylinder, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 4 maths lessons from the 2D and 3D shape: surface area and volume (pyramids, spheres and cones) unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Starter quiz
6 Questions
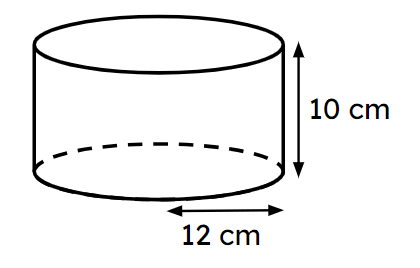
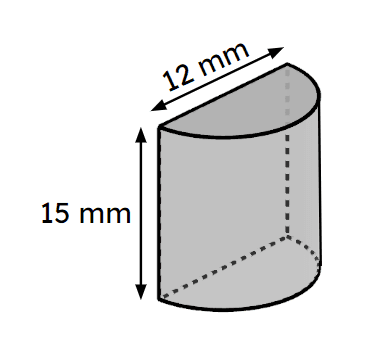
Exit quiz
6 Questions