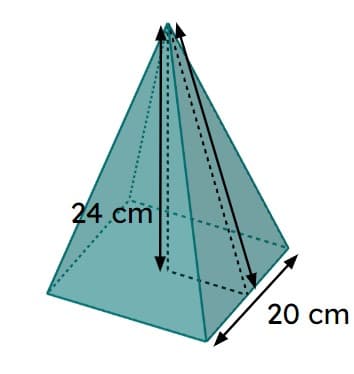
The surface area of a pyramid
I can calculate the surface area of a pyramid.


The surface area of a pyramid
I can calculate the surface area of a pyramid.
These resources will be removed by end of Summer Term 2025.
Lesson details
Key learning points
- There are many different types of pyramid.
- The apex of the pyramid is not necessarily above the centre of the base.
- Although the base is a polygon, the sides are always triangles.
- The surface area of a pyramid is the sum of the area of all the faces.
Keywords
Pyramid - A pyramid is a 3D shape that has a polygonal base and triangular faces that meet at an apex.
Apex - The apex is the point (vertex) which is the greatest perpendicular distance from the base.
Right pyramid - When the apex lies directly above the centre of the base, then it is called a right pyramid.
Oblique pyramid - An oblique pyramid is when the apex is not directly above the centre of the base.
Common misconception
Pupils may think that a cone is a pyramid.
Remind pupils that a pyramid has a polygonal base, so a cone cannot be a pyramid as the base is a circle, which is not a polygon.
To help you plan your year 11 maths lesson on: The surface area of a pyramid, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 11 maths lesson on: The surface area of a pyramid, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 4 maths lessons from the 2D and 3D shape: surface area and volume (pyramids, spheres and cones) unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Starter quiz
6 Questions
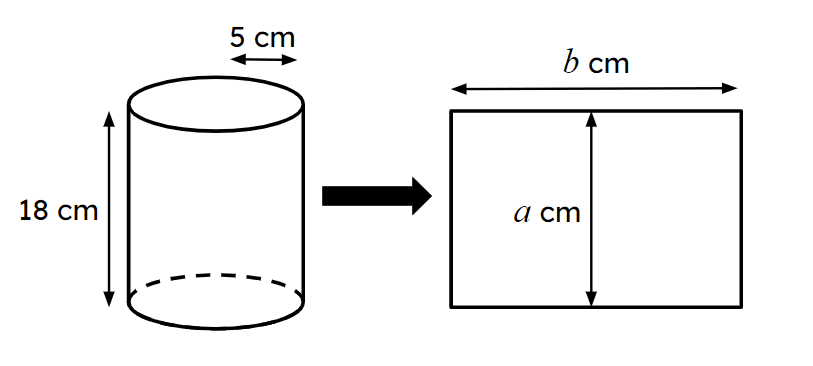
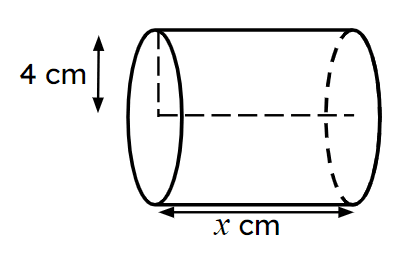
Exit quiz
6 Questions
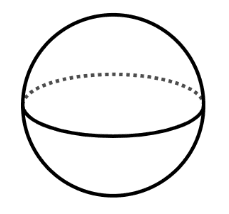
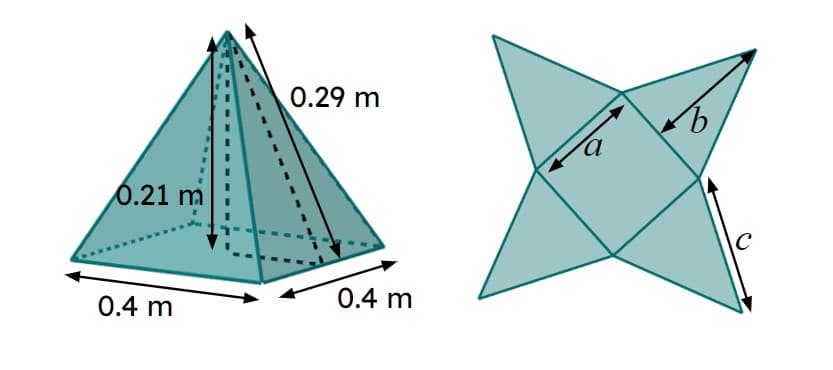
$$a$$ -
0.4 m
$$b$$ -
0.29 m
$$c$$ -
0.352 m (3 s.f.)
not a marked length on the net -
0.21 m