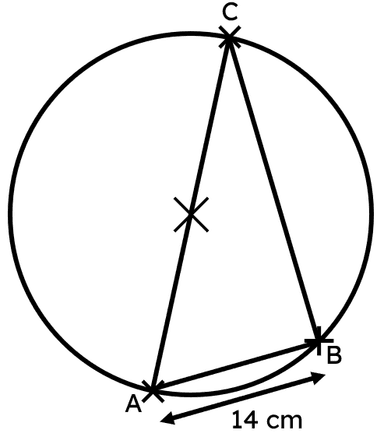
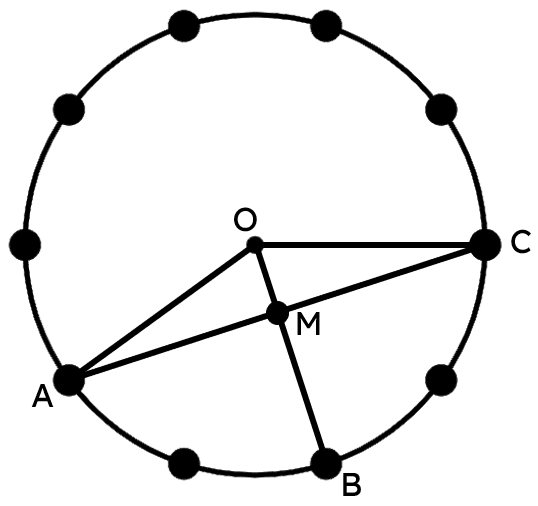
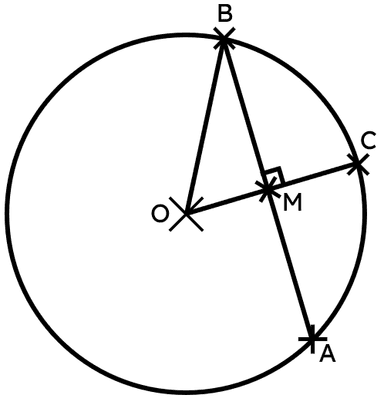
The perpendicular from the centre of a circle to a chord bisects the chord

I can derive and use the theorem: the perpendicular from the centre of a circle to a chord bisects the chord.

Download all resources

Share activities with pupils

New

Year 10

Higher

The perpendicular from the centre of a circle to a chord bisects the chord

I can derive and use the theorem: the perpendicular from the centre of a circle to a chord bisects the chord.

Download all resources

Share activities with pupils

These resources will be removed by end of Summer Term 2025.

Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.

View new resources

Slide deck

Download slide deck

Skip slide deck

Lesson details

Key learning points

A theorem is a statement that can be demonstrated to be true by accepted mathematical operations and arguments
Theorems can be thought of as puzzles to solve, you are showing how to find a result
In order to use this theorem, you may need to draw a diagram or add more information to an existing one

Keywords

Bisect - To bisect means to cut or divide an object into two equal parts.
Chord - A chord is any line segment joining two points on the circumference of a circle.

Common misconception

Pupils may assume that a radius which intersects a chord always bisects the chord.

A radius only bisects a chord if they are perpendicular.

The lesson demonstrates how this circle theorem could be explored practically by using a pair of compasses, using a circular geoboard and using dynamic geometry software. Pupils may wish to explore these further for themselves.