Myths about teaching can hold you back


- Year 11•
- Higher
Experimental probability
I can decide if a game/object is fair and calculate the experimental probability.


- Year 11•
- Higher
Experimental probability
I can decide if a game/object is fair and calculate the experimental probability.
These resources were made for remote use during the pandemic, not classroom teaching.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
Lesson details
Key learning points
- A set of results can be critically evaluated to help determine if a game/object is fair
- Different samples and may affect your perception of fair
- The experimental probability of an outcome/event can be calculated from a set of results
- Experimental probabilities can be used to estimate an event may occur in a set number of trials
Keywords
Experimental probability - The frequency of an outcome from an experiment can be used to produce an experimental probability. This is sometimes referred to as relative frequency.
Fair - A trial or experiment is fair if each outcome has an equal chance of happening. Each outcome is said to be equally likely.
Bias - If there is bias, in a trial or experiment, the outcomes are not equally likely.
Common misconception
If outcome A occurs more often than outcome B, during an experiment, pupils may conclude that outcome A has a greater probability of occurring than outcome B in future trials.
Even when two outcomes are equally likely to happen, one may occur more often than the other due to chance. You could be more confident about your conclusion if you observe a large difference in results in an experiment with a large number of trials.
To help you plan your year 11 maths lesson on: Experimental probability, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 11 maths lesson on: Experimental probability, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 4 maths lessons from the Conditional probability unit, dive into the full secondary maths curriculum, or learn more about lesson planning.

Licence
Prior knowledge starter quiz
6 Questions
Q1.Two or more events are are mutually __________ if they share no common outcome.
Q2.A survey asked people whether they lived in Oakfield or not, and if they last shopped by online delivery or by going in-store. A random person is selected. Match each event to its probability.
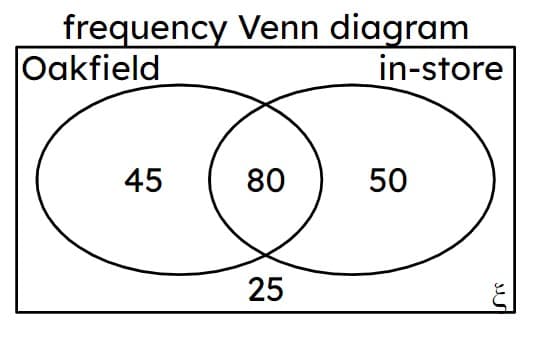
P(lives in Oakfield) -
$$125\over200$$
P(doesn't live in Oakfield) -
$$75\over200$$
P(shops in-store) -
$$130\over200$$
P(shops online) -
$$70\over200$$
P(lives in Oakfield and shops online) -
$$45\over200$$
P(lives in Oakfield and shops in-store) -
$$80\over200$$
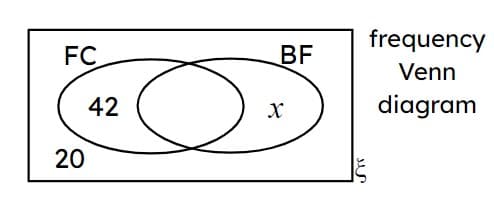
Q3.A swimming club has 80 members. There are 8 members who swim both front crawl (FC) and butterfly (BF). The value of $$x$$ is .
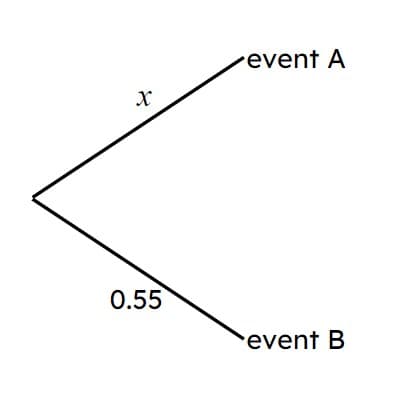
Q4.This probability tree shows the probability of one of two events occurring.
The value of $$x$$ is .
Q5.Lucas and Izzy each play one game of squash that they can either win or lose. P(Lucas wins) = 0.6, P(Izzy wins) = 0.7. Use the probability tree to find the probability that they both win their game.
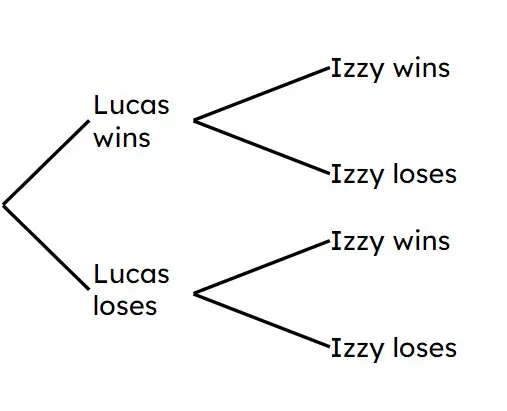
Q6.Lucas and Izzy each play one game of squash that they can either win or lose. P(Lucas wins) = 0.6, P(Izzy wins) = 0.7. The probability that at least one of them wins their match is .

Assessment exit quiz
6 Questions
Q1.An probability can be determined by the number of times an event occurred during multiple trials.
Q2.Select the biased spinners.
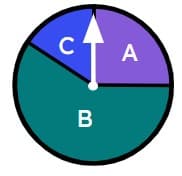

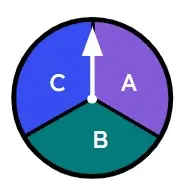
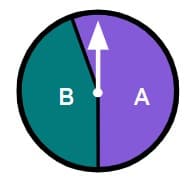
Q3.A toy brick that is dropped could land in one of four possible ways. Sofia drops the toy brick multiple times. Starting with the least likely outcome, place the outcomes in order of likelihood.
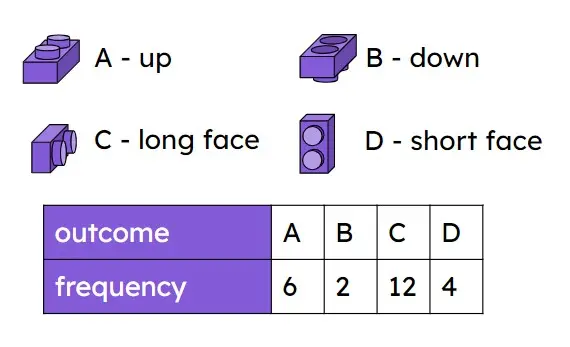
Q4.A toy brick that is dropped could land in one of four possible ways. Sofia drops the toy brick multiple times. How can Sofia improve her experiment to make it more accurate?

Q5.A dropped cone could land in one of two ways. The bar chart shows the results from an experiment. Which calculation shows how to find the experimental probability of the cone landing base down?
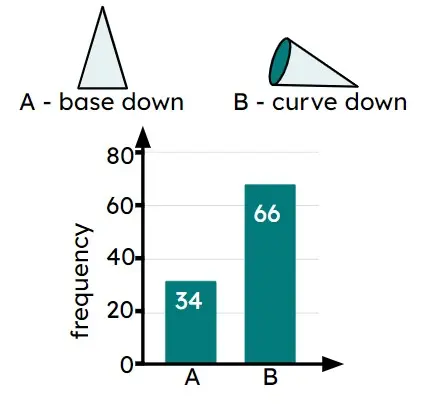
Q6.A dropped cone could land in one of two ways. The bar chart shows the results from an experiment. In an experiment with 200 trials you should expect the cone to land base down times.


