Skip to content
Oak National Academy
Oak National Academy
Teachers
Pupils
icon-background-square
New
New
Year 11
Higher

Problem solving with iteration

I can use my knowledge of iteration to solve problems.

Download all resources
arrow-right
Share activities with pupils
arrow-right
icon-background-square
New
New
Year 11
Higher

Problem solving with iteration

I can use my knowledge of iteration to solve problems.

Download all resources
arrow-right
Share activities with pupils
arrow-right
warning

These resources will be removed by end of Summer Term 2025.

Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
View new resources
arrow-right

Lesson details

Key learning points

  1. Quadratics can have their solutions estimated using iteration
  2. This can be helpful to quickly determine where the solutions are likely to be
  3. It can be used to check any solutions

Keywords

  • Iteration - Iteration is the repeated application of a function or process in which the output of each iteration is used as the input for the next iteration.

Common misconception

An iterative formula can always be used to find the solutions to an equation.

This lesson addresses limitations of iteration. Some formulas will cause an error becasue we are unable to evaluate the square root of a negative or divide by 0. Other formulas may not converge. Different values of $$x_0$$ produce different results.


To help you plan your year 11 maths lesson on: Problem solving with iteration, download all teaching resources for free and adapt to suit your pupils' needs...

This lesson is all about exploring the limitations of iteration. Graphing software will be useful for pupils to explore different formulae and differnt values on $$x_0$$. These equations are all quadratics so pupils can use calculators or the quadratic formula to find or check solutions.
speech-bubble
Teacher tip
copyright

Licence

This content is © Oak National Academy Limited (2025), licensed on Open Government Licence version 3.0 except where otherwise stated. See Oak's terms & conditions (Collection 2).

Lesson video

Skip lesson video

Loading...

Starter quiz

Download starter quiz

6 Questions

Q1.
What are the solutions to the quadratic equation $$x^2-3x-10=0$$?
$$x=-3$$ and $$x=-10$$
$$x=3$$ and $$x=-10$$
$$x=-2$$ and $$x=-5$$
$$x=2$$ and $$x=-5$$
Correct answer: $$x=-2$$ and $$x=5$$
Q2.
What are the approximate solutions to the quadratic equation $$x^2+2x-5=0$$ ?
$$x=1.22$$ and $$x=-2.68$$ to 3 significant figures
$$x=-1.22$$ and $$x=2.68$$ to 3 significant figures
Correct answer: $$x=1.45$$ and $$x=-3.45$$ to 3 significant figures
$$x=-1.45$$ and $$x=3.45$$ to 3 significant figures
Q3.
Which value does the iterative formula $$x_{n+1}=\frac{8}{x_n-2}$$ converge on to 1 significant figure when $$x_0=5$$ ?
-3
Correct answer: -2
-1
0.8
12
Q4.
Using the iterative formula $$x_{n+1}=\frac{(x_n)^3+1}{2}$$ and $$x_0=0$$ , which of these is a solution to $$x^3-2x+1=0$$ correct to 2 significant figures?
$$x=0.56$$
$$x=0.59$$
Correct answer: $$x=0.62$$
$$x=0.67$$
Q5.
Between which sets of values is there definitely a solution to $$x^2-5x-1=0$$ ?
Between $$x=-2$$ and $$x=-1$$
Correct answer: Between $$x=-1$$ and $$x=0$$
Between $$x=4.8$$ and $$x=4.9$$
Correct answer: Between $$x=5.1$$ and $$x=5.2$$
Q6.
Which of these are solutions to $$x^2+2x-6=0$$ correct to the stated degree of accuracy?
Correct answer: $$x=2$$ to 1 significant figure
$$x=1.5$$ to 2 significant figure
$$x=-3$$ to 1 significant figure
Correct answer: $$x=-4$$ to 1 significant figure

Exit quiz

Download exit quiz

6 Questions

Q1.
Laura has used the equation $$x^2+x-12=0$$ to write the iterative formula $$x_{n+1}=12-(x_n)^2$$. If 3 is an exact solution, what should happen when she uses $$x_0=3$$?
An error will occur.
The first iteration will equal 0.
Correct answer: The first iteration will equal 3.
The outputs of the formula will eventually converge on 3.
The iterative formula will not converge.
Q2.
Which of these could be iterative formulae to find a solution to the equation $$x^2-5x+4=0$$?
$$x_{n+1} = \sqrt{4-5x_n}$$
$$x_{n+1} = -\sqrt{5x_n+4}$$
$$x_{n+1}=\frac{(x_n)^2}{5} +4$$
Correct answer: $$x_{n+1}=-\frac{4}{x_n-5}$$
Q3.
Which of these could be iterative formulae to find a solution to the equation $$x^2+2x-6=0$$?
Correct answer: $$x_{n+1}=\frac{6}{x_n+2} $$
Correct answer: $$x_{n+1}=3-\frac{(x_n)^2}{2} $$
$$x_{n+1} = \sqrt{2x_n-6}$$
$$x_{n+1} = (x_n)^2+2(x_n)-6$$
Q4.
Using the iterative formula $$x_{n+1}=\frac{6}{x_n+2} $$ which values of $$x_0$$ converge on a solution to the equation $$x^2+2x-6=0$$ ?
$$x_0=-5$$
Correct answer: $$x_0=-3$$
$$x_0=-2$$
Correct answer: $$x_0=0$$
Correct answer: $$x_0=2$$
Q5.
Which of these iterative formulae converge on the approximate solution $$x=0.459$$ to the equation $$x^2-7x+3=0$$ when $$x_0=2$$?
Correct answer: $$x_{n+1}=-\frac{3}{x_n-7}$$
$$x_{n+1}=\sqrt{7x_n-3}$$
$$x_{n+1}=-\sqrt{7x_n-3}$$
Correct answer: $$x_{n+1}=\frac{(x_n)^2+3}{7}$$
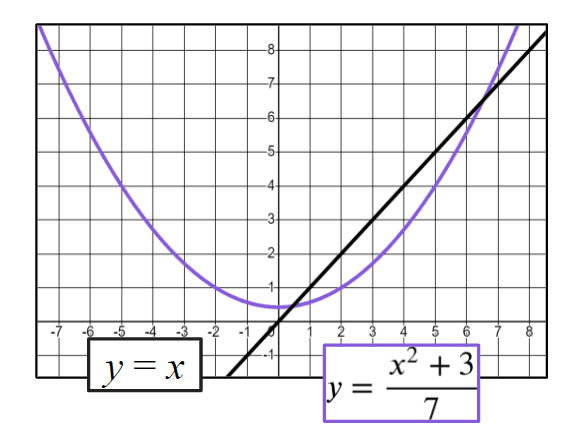
Q6.
Using the graph (or otherwise) which values of $$x_0$$ will converge on a solution to the equation $$x^2-7x+3=0$$ using the iterative formula $$x_{n+1}=\frac{(x_n)^2+3}{7}$$?
An image in a quiz
$$x_0=-7$$
Correct answer: $$x_0=-5$$
Correct answer: $$x_0=0$$
Correct answer: $$x_0=5$$
$$x_0=8$$