New
New
Year 10
Higher
Checking and securing understanding of drawing linear graphs
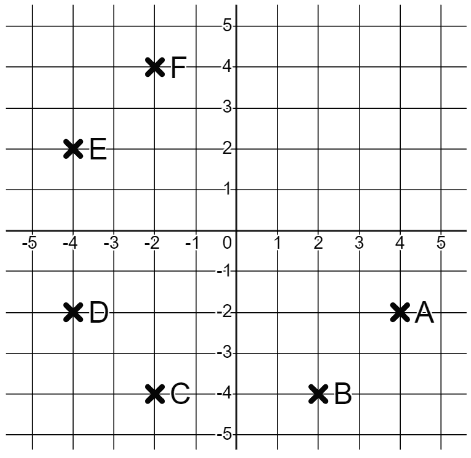
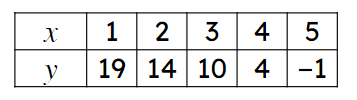
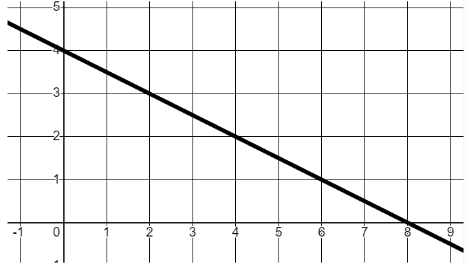
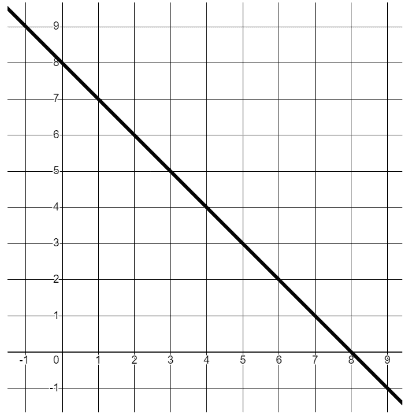
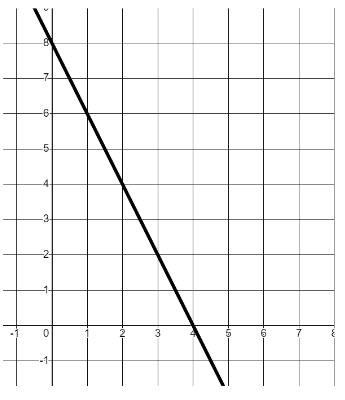
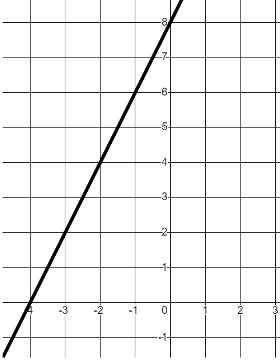
I can draw a linear graph from its equation and relate the features of the graph to its equation.
New
New
Year 10
Higher
Checking and securing understanding of drawing linear graphs
I can draw a linear graph from its equation and relate the features of the graph to its equation.
Lesson details
Video
Loading...
Starter quiz
Download starter quiz
6 Questions
Exit quiz
Download exit quiz