- Year 11•
- Higher
The cosine rule
I can derive the formula for the cosine rule.
- Year 11•
- Higher
The cosine rule
I can derive the formula for the cosine rule.
These resources will be removed by end of Summer Term 2025.
Switch to our new teaching resources now - designed by teachers and leading subject experts, and tested in classrooms.
These resources were created for remote use during the pandemic and are not designed for classroom teaching.
Lesson details
Key learning points
- There are multiple ways to prove the cosine rule
- When deriving (or proving) it is sometimes useful to derive other information
Keywords
Cosine rule - The cosine rule is a formula used for calculating either an unknown side length or the size of an unknown angle.
Common misconception
Pupils may not see the need for this rule as they have the sine rule.
The sine rule can be used in many cases but it is not always the most efficient. There will be problems where it will be much faster to use the cosine rule.
To help you plan your year 11 maths lesson on: The cosine rule, download all teaching resources for free and adapt to suit your pupils' needs...
To help you plan your year 11 maths lesson on: The cosine rule, download all teaching resources for free and adapt to suit your pupils' needs.
The starter quiz will activate and check your pupils' prior knowledge, with versions available both with and without answers in PDF format.
We use learning cycles to break down learning into key concepts or ideas linked to the learning outcome. Each learning cycle features explanations with checks for understanding and practice tasks with feedback. All of this is found in our slide decks, ready for you to download and edit. The practice tasks are also available as printable worksheets and some lessons have additional materials with extra material you might need for teaching the lesson.
The assessment exit quiz will test your pupils' understanding of the key learning points.
Our video is a tool for planning, showing how other teachers might teach the lesson, offering helpful tips, modelled explanations and inspiration for your own delivery in the classroom. Plus, you can set it as homework or revision for pupils and keep their learning on track by sharing an online pupil version of this lesson.
Explore more key stage 4 maths lessons from the Non right-angled trigonometry unit, dive into the full secondary maths curriculum, or learn more about lesson planning.
Licence
Lesson video
Loading...
Prior knowledge starter quiz
6 Questions
Q1.Which of the following are equivalent to $$\cos(\theta°)=\frac{\text{adj}}{\text{hyp}}$$?
Q2.Match the trigonometric ratio with the correct definition.
The sine of an angle is the -
$$y$$-coordinate of P on the triangle formed inside the unit circle.
The cosine of an angle is the -
$$x$$-coordinate of P on the triangle formed inside the unit cirlce.
The tangent is the -
line that intersects the circle exactly once.
Q3.Match the following values.
1 -
$$\cos(0°)$$
$$\frac{\sqrt{3}}{2}$$ -
$$\cos(30°)$$
$$\frac{\sqrt{2}}{2}$$ -
$$\cos(45°)$$
0.5 -
$$\cos(60°)$$
0 -
$$\cos(90°)$$
-0.174 (3 s.f) -
$$\cos(100°)$$
Q4.A right-angled triangle has a height of 15 cm and a hypotenuse of 17 cm. Work out the area.
Q5.An isosceles triangle has a base of 16 cm and base angles of 53.97° (2 d.p). The area of this triangle, given to 2 significant figures, is cm$$^2$$.
Q6.Six equilateral triangles are put together to make a regular hexagon. The length of each triangle is 10 cm. Work out the exact area of the regular hexagon.
Assessment exit quiz
6 Questions
Q1.Match the correct rules, theorem or formulae.
Pythagoras' theorem -
$$a^2+b^2=c^2$$
The sine rule -
$$\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$$
The cosine rule -
$$a^2 = b^2+c^2-2bc\cos(A)$$
Area of a triangle -
$$\frac{1}{2}ab\sin(C)$$
Q2.Which of the following are the cosine rule?
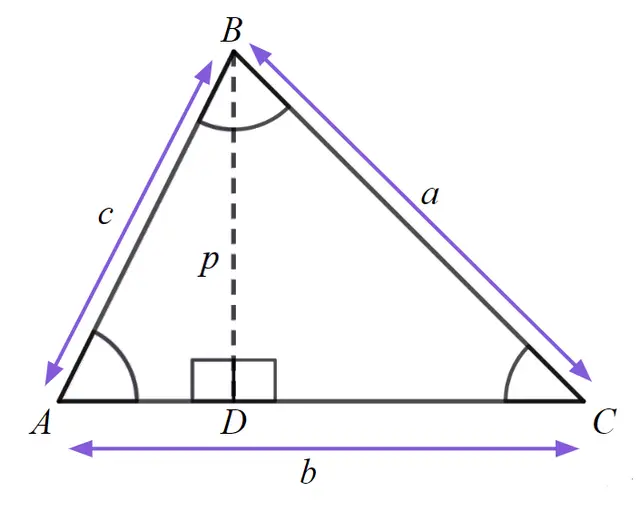
Q3.A triangle has adjacent lengths of 16 cm and 20 cm with an angle in between of 55°. Work out the missing length to 1 decimal place.
Q4.This proof has been mixed up. Write each line in order, starting with $$p^2 + (b - r)^2 = a^2$$.
Q5.Given a triangle with lengths labelled $$a$$, $$b$$ and $$c$$, match up the length $$b$$ with dimensions of the triangle and the angle $$B$$.
10.6 cm -
$$a=8$$ cm, $$B=36$$° and $$c=16$$ cm
11.8 cm -
$$a=16$$ cm, $$B=36$$° and $$c=20$$ cm
4.9 cm -
$$a=8$$ cm, $$B=36$$° and $$c=8$$ cm
12.2 cm -
$$a=8$$ cm, $$B=72$$° and $$c=12$$ cm
Q6.Given a triangle with lengths labelled $$a$$, $$b$$ and $$c$$, match up the angle $$B$$ with the dimensions of the triangle.
46.57° -
$$a=8$$ cm, $$b=12$$ cm and $$c=16$$ cm
36.87° -
$$a=16$$ cm, $$b=12$$ cm and $$c=20$$ cm
97.18° -
$$a=8$$ cm, $$b=12$$ cm and $$c=8$$ cm
70.53° -
$$a=8$$ cm, $$b=12$$ cm and $$c=12$$ cm